搜索
【题目】（8分）如图，平行四边形ABCD中，对角线AC、BD相交于点O，若E、F是AC上两动点，分别从A、C两点以相同的速度1cm/s向C、A运动．
（1）四边形DEBF是平行四边形吗？请说明理由；
（2）若BD=12cm，AC=16cm，当运动时间t为何值时，四边形DEBF是矩形？
参考答案：
【答案】（1）是；（2）t=2或16﹣2=14
【解析】整体分析：
（1）根据对角线互相平分的四边形是平行四边形判断；（2）根据EF=BD=12，分两种情况列出关于t的方程求解.
解：（1）是．
理由：在平行四边形ABCD中，则OD=OB，OA=OC，
∵E、F两点移动的速度相同，即AE=CF，
∴OE=OF，
又∵OD=OB
∴四边形DEBF是平行四边形；
（2）因为矩形对角线相等，所以当EF=12时，其为矩形，
即16-2t=12，或2t-16=12，
解得t=2或t=14.
所以当t=2或14时，四边形DEBF是矩形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，若把边长为1的正方形ABCD的四个角（阴影部分）剪掉，得一四边形A1B1C1D1 ． 试问怎样剪，才能使剩下的图形仍为正方形，且剩下图形的面积为原来正方形面积的
，请说明理由．（写出证明及计算过程） 
-
科目： 来源： 题型：
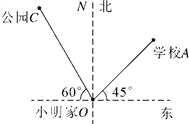
查看答案和解析>>【题目】小明家O，学校A和公园C的平面示意图如图所示，图上距离OA＝2cm，OC＝2.5cm.
(1)学校A、公园C分别在小明家O的什么方向上？
(2)若学校A到小明家O的实际距离是400m，求公园C到小明家O的实际距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以AB为直径的⊙O经过点P，C是⊙O上一点，连接PC交AB于点E，且∠ACP=60°，PA=PD．
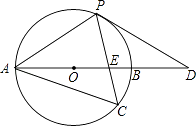
（1）试判断PD与⊙O的位置关系，并说明理由；
（2）若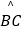
： 
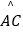=1：2，求AE：EB：BD的值（请你直接写出结果）；
（3）若点C是弧AB的中点，已知AB=4，求CECP的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标平面中，O为原点，点A的坐标为（20，0），点B在第一象限内，BO=10，sin∠BOA=
． 
（1）在图中，求作△ABO的外接圆（尺规作图，不写作法但需保留作图痕迹）；
（2）求点B的坐标与cos∠BAO的值；
（3）若A，O位置不变，将点B沿x轴向右平移使得△ABO为等腰三角形，请求出平移后点B的坐标． -
科目： 来源： 题型：
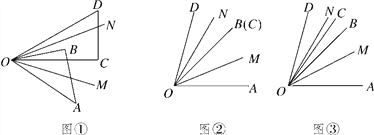
查看答案和解析>>【题目】如图①，将一副三角板的两个锐角顶点放到一块，∠AOB＝45°，∠COD＝30°，OM，ON分别是∠AOC，∠BOD的平分线．
(1)当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图②)，则∠MON的大小为________；
(2)如图③，在(1)的条件下，继续绕着点O逆时针旋转∠COD，当∠BOC＝10°时，求∠MON的大小，写出解答过程；
(3)在∠COD绕点O逆时针旋转过程中，∠MON＝________°.
-
科目： 来源： 题型：
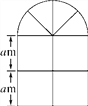
查看答案和解析>>【题目】（12分）如图是某种窗户的形状，其上部是半圆形，下部是边长相同的四个小正方形，已知下部的小正方形的边长为am，计算：
（1）窗户的面积；
（2）窗框的总长；
（3）若a＝1，窗户上安装的是玻璃，玻璃每平方米25元，窗框每米20元，窗框的厚度不计，求制作这种窗户需要的费用是多少元（π取3.14，结果保留整数）.
相关试题
