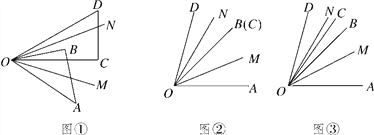
【题目】如图①,将一副三角板的两个锐角顶点放到一块,∠AOB=45°,∠COD=30°,OM,ON分别是∠AOC,∠BOD的平分线.
(1)当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图②),则∠MON的大小为________;
(2)如图③,在(1)的条件下,继续绕着点O逆时针旋转∠COD,当∠BOC=10°时,求∠MON的大小,写出解答过程;
(3)在∠COD绕点O逆时针旋转过程中,∠MON=________°.
参考答案:
【答案】(1)37.5°;(2)∠MON=37.5°;(3)37.5°
【解析】试题分析:(1)、根据角平分线的性质得出∠NOC=15°,∠MOC=22.5°,最后根据∠MON=∠NOC+∠MOC得出答案;(2)、首先根据∠BOC的度数求出∠AOC和∠BOD的度数,然后根据角平分线的性质求出∠BON和∠MOB的度数,最后根据∠MON=∠MOB+∠BON得出答案;(3)、根据题意得出∠AOC=∠AOB+∠BOC,∠BOD=∠COD+∠BOC,根据角平分线的性质得出∠MOC=![]() (∠AOB+∠BOC),∠CON=
(∠AOB+∠BOC),∠CON=![]() ∠BOD-∠BOC,最后根据∠MON=∠MOC+∠CON得出答案.
∠BOD-∠BOC,最后根据∠MON=∠MOC+∠CON得出答案.
试题解析:解:(1)、37.5°;
(2)、当绕着点O逆时针旋转∠COD,∠BOC=10°时,∠AOC=55°,∠BOD=40°,
∴∠BON=![]() ∠BOD=20°, ∠MOB=
∠BOD=20°, ∠MOB=![]() ∠AOC-∠BOC=27.5°-10°=17.5°,
∠AOC-∠BOC=27.5°-10°=17.5°,
∴∠MON=∠MOB+∠BON=17.5°+20°=37.5°;
(3)、解析:∠AOC=∠AOB+∠BOC,∠BOD=∠COD+∠BOC,
又OM,ON分别是∠AOC,∠BOD的平分线,∠AOB=45°,∠COD=30°,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (∠AOB+∠BOC),
(∠AOB+∠BOC),
∠CON=![]() ∠BOD-∠BOC,
∠BOD-∠BOC,
∴∠MON=∠MOC+∠CON=![]() (∠AOB+∠BOC)+
(∠AOB+∠BOC)+![]() ∠BOD-∠BOC=
∠BOD-∠BOC=![]() ∠AOB+
∠AOB+![]() (∠BOD-∠BOC)=
(∠BOD-∠BOC)=![]() ∠AOB+
∠AOB+![]() ∠COD=37.5°.
∠COD=37.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD.
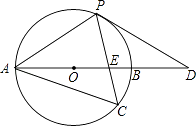
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若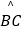 :
: 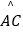 =1:2,求AE:EB:BD的值(请你直接写出结果);
=1:2,求AE:EB:BD的值(请你直接写出结果);
(3)若点C是弧AB的中点,已知AB=4,求CECP的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向C、A运动.
(1)四边形DEBF是平行四边形吗?请说明理由;
(2)若BD=12cm,AC=16cm,当运动时间t为何值时,四边形DEBF是矩形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=
 .
. 
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴向右平移使得△ABO为等腰三角形,请求出平移后点B的坐标. -
科目: 来源: 题型:
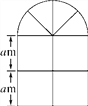
查看答案和解析>>【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.

(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.

相关试题

