搜索
【题目】
（1）计算：（a﹣b）（a2+ab+b2）
（2）利用所学知识以及（1）所得等式，分解因式：m3﹣n3﹣3mn（m﹣n）
参考答案：
【答案】（1）a3﹣b3；（2）（m﹣n）3.
【解析】
（1）根据多项式乘以多项式的法则进行计算即可；
（2）利用分组分解法，先将前两项分为一组，根据（1）的立方差公式分解因式，再提公因式即可．
解：（1）原式=a3+a2b+ab2﹣a2b﹣ab2﹣b3
=a3﹣b3；
（2）原式=（m﹣n）（m2+mn+n2）﹣3mn（m﹣n）
=（m﹣n）（m2﹣2mn+n2）
=（m﹣n）3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ABC=90°，AB=3，BC=4，AD是∠BAC的平分线．
（1）尺规作图：过点D作DE⊥AC于E；
（2）求DE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列多项式乘法中，可用平方差公式计算的是（ ）
A.（2a+b）（2a﹣3b）
B.（x+1）（1+x）
C.（x﹣2y）（x+2y）
D.（﹣x﹣y）（x+y） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A、F、C、D在同一条直线上，已知AF=DC，∠A=∠D，BC∥EF，求证：AB=DE．
【答案】证明见解析．
【解析】试题分析：欲证明AB=DE，只要证明△ABC≌△DEF即可．
试题解析：∵AF=CD，
∴AC=DF，
∵BC∥EF，
∴∠ACB=∠DFE，
在△ABC和△DEF中，
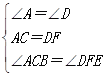，∴△ABC≌△DEF（ASA），
∴AB=DE．
考点：全等三角形的判定与性质．
【题型】解答题
【结束】
25【题目】如图，
，AE=BD，点D在AC边上， 
，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若
，求BDE的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知⊙O为△ABC的外接圆，BC为直径，点E在AB上，过点E作EF⊥BC，点G在FE的延长线上，且GA＝GE.
(1)判断AG与⊙O的位置关系，并说明理由。
(2)若AC＝6，AB＝8，BE＝3，求线段OE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．
（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6
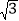，AF=4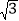，求AE的长．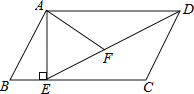
-
科目： 来源： 题型：
查看答案和解析>>【题目】某超市用3 000元购进某种干果销售，由于销售状况良好，超市又调拨9 000元购进该种干果，但这次的进价比第一次的进价提高了20%，购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售，当大部分干果售出后，余下的600 kg按售价的八折售完．
(1)该种干果第一次的进价是多少？
(2)超市销售这种干果共盈利多少元？
相关试题
