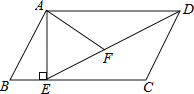
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
参考答案:
【答案】(1)详见解析;(2)6
【解析】试题分析:(1)证明:∵平行四边形ABCD,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.(1分)
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C. (2分)
在△ADF与△DEC中,
![]() ∴△ADF∽△DEC.(3分)
∴△ADF∽△DEC.(3分)
(2)解:∵平行四边形ABCD,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴![]() ,∴DE=
,∴DE=![]() =
=![]() =12.(5分)
=12.(5分)
在Rt△ADE中,由勾股定理得:AE=![]() =
=![]() =6.
=6.
考点: 1.三角形的相似;2.勾股定理
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF,求证:AB=DE.

【答案】证明见解析.
【解析】试题分析:欲证明AB=DE,只要证明△ABC≌△DEF即可.
试题解析:∵AF=CD,
∴AC=DF,
∵BC∥EF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
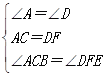 ,
,∴△ABC≌△DEF(ASA),
∴AB=DE.
考点:全等三角形的判定与性质.
【题型】解答题
【结束】
25【题目】如图,
 ,AE=BD,点D在AC边上,
,AE=BD,点D在AC边上,  ,AE和BD相交于点O.
,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若
 ,求BDE的度数.
,求BDE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:(a﹣b)(a2+ab+b2)
(2)利用所学知识以及(1)所得等式,分解因式:m3﹣n3﹣3mn(m﹣n)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)判断AG与⊙O的位置关系,并说明理由。
(2)若AC=6,AB=8,BE=3,求线段OE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨9 000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售,当大部分干果售出后,余下的600 kg按售价的八折售完.
(1)该种干果第一次的进价是多少?
(2)超市销售这种干果共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:
 ,
,  ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:  ,
,  .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如:  ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:  .
.(1)将分式
 化为带分式;
化为带分式;(2)当x取哪些整数值时,分式
 的值也是整数?
的值也是整数?(3)当x的值变化时,分式
 的最大值为 .
的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:
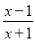 ,
, 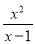 ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: 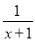 ,
, 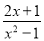 .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: 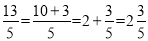 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如: 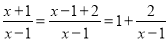 .
.(1)将分式
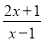 化为带分式;
化为带分式;(2)当x取哪些整数值时,分式
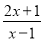 的值也是整数?
的值也是整数?(3)当x的值变化时,分式
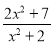 的最大值为 .
的最大值为 .【答案】(1)2+
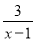 ;(2)x=0,2,﹣2,4;(3)
;(2)x=0,2,﹣2,4;(3)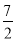 .
.【解析】试题分析:(1)仿照阅读材料中的方法加你个原式变形即可;
(2)原式变形后,根据结果为整数确定出整数x的值即可;
(3)原式变形后,确定出分式的最大值即可.
试题解析:(1)原式=
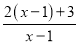 =2+
=2+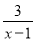 ;
;(2)由(1)得:
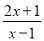 =2+
=2+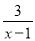 ,
,要使
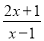 为整数,则
为整数,则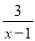 必为整数,
必为整数,∴x﹣1为3的因数,
∴x﹣1=±1或±3,
解得:x=0,2,﹣2,4;
(3)原式=
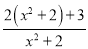 =2+
=2+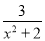 ,
,当x2=0时,原式取得最大值
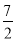 .
.故答案为:
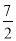 .
.【题型】解答题
【结束】
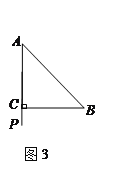
28【题目】已知,△ABC中,AC=BC,∠ACB=90°,点P在射线AC上,连接PB,将线段PB绕点B逆时针旋转90°得线段BN,AN交直线BC于M.
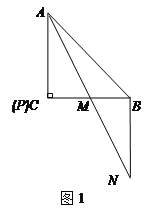
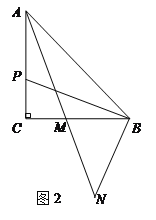
(1)图1,若点P与点C重合,则
 =______,
=______,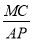 =______.(直接写出结果)
=______.(直接写出结果)(2)图2,若点P在线段AC上,求证: AP=2MC;
(3)图3,若点P在线段AC的延长线上,完成图形,并直接写出
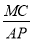 =______.
=______.
相关试题

