【题目】定义:可以表示为两个互质整数的商的形式的数称为有理数,整数可以看作分母为1的有理数;反之为无理数.如![]() 不能表示为两个互质的整数的商,所以
不能表示为两个互质的整数的商,所以![]() 几个号无理数.可以这样证明:
几个号无理数.可以这样证明:
设![]() ,a与b是互质的两个整数,且b≠0,则2=
,a与b是互质的两个整数,且b≠0,则2=![]() ,所以a=2b.
,所以a=2b.
因为b是整数且不为0,所以a是不为0的偶数.设a=2n(n是整数),
所以b=2n,所以b也是偶数,与a与b是互质的整数矛盾,
所以![]() 是无理数.
是无理数.
仔细阅读上文,然后请证明:![]() 是无理数。
是无理数。
参考答案:
【答案】证明见解析.
【解析】
先设![]() ,由已知条件a与b是互质的两个整数,且b≠0,则5=
,由已知条件a与b是互质的两个整数,且b≠0,则5=![]() 可得:a不为0且为5的倍数,再设a=5n,(n是整数),则b2=5n2,从而得到b也为5的倍数,与a,b是互质的正整数矛盾,从而证明了答案.
可得:a不为0且为5的倍数,再设a=5n,(n是整数),则b2=5n2,从而得到b也为5的倍数,与a,b是互质的正整数矛盾,从而证明了答案.
设![]() ,a与b是互质的两个整数,且b≠0,则5=
,a与b是互质的两个整数,且b≠0,则5=![]() ,
,
所以a=5b.
∵a,b是整数且不为0,
∴a为5的倍数。设a=5n(n是整数),
∴b=5n,
∴b也是5的位数,与a与b是互质的整数矛盾,
∴![]() 是无理数。
是无理数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按如下步骤作图: ①分别以A,C为圆心,大于
 AC的长为半径画弧,两弧交于P,Q两点;
AC的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若x,y都是实数,且
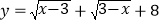 ,求5x+13y+6的立方根;
,求5x+13y+6的立方根;(2)已知△ABC的三边长分别为a,b,c,且满足
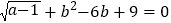 ,求c的取值范围。
,求c的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条 “折线数轴” .图中点A表示-11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、B两点在数轴上相距的长度与Q、O两点在数轴上相距的长度相等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】.. 计算题:
(1)8﹣(﹣10)﹣|﹣2|
(2)2
 ﹣3
﹣3 +(﹣3
+(﹣3 )﹣(+5
)﹣(+5 )
)(3)﹣24×(﹣
 +
+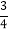 ﹣
﹣ )
)(4)﹣49
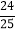 ×10(简便运算)
×10(简便运算)(5)﹣
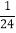 ÷(
÷( ﹣
﹣ +
+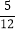 )
)(6)3×(﹣38
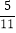 )﹣4×(﹣38
)﹣4×(﹣38 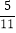 )﹣38
)﹣38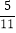
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了方便居民低碳出行,2015年12月30日,湘潭市公共自行车租赁系统(一期)试运行以来,越来越多的居民选择公共自行车作为出行的交通工具,市区某中学课外兴趣小组为了了解某小区居民出行方式的变化情况,随机抽取了该小区部分居民进行调查,并绘制了如图的条形统计图和扇形统计图(部分信息未给出).

请根据上面的统计图,解答下列问题:
(1)被调查的总人数是人;
(2)公共自行车租赁系统运行后,被调查居民选择自行车作为出行方式的百分比提高了多少?
(3)如果该小区共有居民2000人,公共自行车租赁系统运行后估计选择自行车作为出行方式的有多少人?
相关试题

