【题目】如图①,将一副三角板的两个锐角顶点放到一块,∠AOB=45°,∠COD=30°,OM,ON分别是∠AOC,∠BOD的平分线.
(1)当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图②),则∠MON的大小为________;
(2)如图③,在(1)的条件下,继续绕着点O逆时针旋转∠COD,当∠BOC=10°时,求∠MON的大小,写出解答过程;
(3)在∠COD绕点O逆时针旋转过程中,∠MON=________°.

参考答案:
【答案】(1)37.5°;(2)∠MON=37.5°;(3)37.5°
【解析】试题分析:(1)、根据角平分线的性质得出∠NOC=15°,∠MOC=22.5°,最后根据∠MON=∠NOC+∠MOC得出答案;(2)、首先根据∠BOC的度数求出∠AOC和∠BOD的度数,然后根据角平分线的性质求出∠BON和∠MOB的度数,最后根据∠MON=∠MOB+∠BON得出答案;(3)、根据题意得出∠AOC=∠AOB+∠BOC,∠BOD=∠COD+∠BOC,根据角平分线的性质得出∠MOC=![]() (∠AOB+∠BOC),∠CON=
(∠AOB+∠BOC),∠CON=![]() ∠BOD-∠BOC,最后根据∠MON=∠MOC+∠CON得出答案.
∠BOD-∠BOC,最后根据∠MON=∠MOC+∠CON得出答案.
试题解析:解:(1)、37.5°;
(2)、当绕着点O逆时针旋转∠COD,∠BOC=10°时,∠AOC=55°,∠BOD=40°,
∴∠BON=![]() ∠BOD=20°, ∠MOB=
∠BOD=20°, ∠MOB=![]() ∠AOC-∠BOC=27.5°-10°=17.5°,
∠AOC-∠BOC=27.5°-10°=17.5°,
∴∠MON=∠MOB+∠BON=17.5°+20°=37.5°;
(3)、解析:∠AOC=∠AOB+∠BOC,∠BOD=∠COD+∠BOC,
又OM,ON分别是∠AOC,∠BOD的平分线,∠AOB=45°,∠COD=30°,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (∠AOB+∠BOC),
(∠AOB+∠BOC),
∠CON=![]() ∠BOD-∠BOC,
∠BOD-∠BOC,
∴∠MON=∠MOC+∠CON=![]() (∠AOB+∠BOC)+
(∠AOB+∠BOC)+![]() ∠BOD-∠BOC=
∠BOD-∠BOC=![]() ∠AOB+
∠AOB+![]() (∠BOD-∠BOC)=
(∠BOD-∠BOC)=![]() ∠AOB+
∠AOB+![]() ∠COD=37.5°.
∠COD=37.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
(1)求证:△ADG≌△CDE;
(2)当CE平分∠ACD时,求tan∠AGD.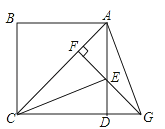
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=10cm,AM=3cm,求CN的长;
(2)如果MN=6cm,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家O,学校A和公园C的平面示意图如图所示,图上距离OA=2cm,OC=2.5cm.
(1)学校A、公园C分别在小明家O的什么方向上?
(2)若学校A到小明家O的实际距离是400m,求公园C到小明家O的实际距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a3﹣2a2b+ab2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:优秀;B:良好;C:合格;D:一般;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:(1)本次调查中,王老师一共调查了多少名同学?
(2)将上面的条形统计图补充完整;并求出“D”所占的圆心角的度数;
(3)从被调查的A类和D类学生中分别选取一位同学进行“一对一”互助学习,请求出所选两位同学恰好是一位男同学和一位女同学的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=60厘米.
(1)点P沿线段AB自A点向B点以4厘米/分的速度运动,同时点Q沿线段自B点向A点以6厘米/分的速度运动,几分钟后,P、Q两点相遇?
(2)几分钟后,P、Q两点相距20厘米?

相关试题

