【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C2017 . 若点P是第2016段抛物线的顶点,则P点的坐标为 . 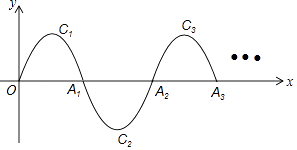
参考答案:
【答案】(﹣1,0)
【解析】解:由题意可知:
第1段抛物线的顶点坐标为:(1,0),
第2段抛物线的顶点坐标为:(﹣1,0),
第3段抛物线的顶点坐标为:(1,0)
故第2016段抛物线的顶点为:(﹣1,0)
所以答案是:(﹣1,0)
【考点精析】认真审题,首先需要了解二次函数图象的平移(平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减),还要掌握抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.)的相关知识才是答题的关键.
-
科目: 来源: 题型:
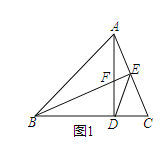
查看答案和解析>>【题目】如图1,在锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,且BF=AC。求证:ED平分∠FEC。
-
科目: 来源: 题型:
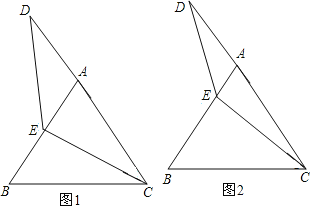
查看答案和解析>>【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:AD BE;
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底角为72°,腰AB的垂直平分线交另一腰AC于点E,垂足为D,连接BE,则下列结论错误的是( )
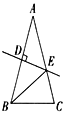
A. ∠EBC为36° B. BC = AE
C. 图中有2个等腰三角形 D. DE平分∠AEB
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
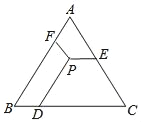
A. 18B. 9
C. 6D. 条件不够,不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,AB=5, AE平分∠DAB交BC所在直线于点E,CE=2,则AD=_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=
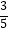 .
.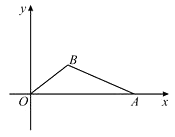
(1)①在图中,求作△ABO的外接圆;(尺规作图,不写作法但需保留作图痕迹);②求点B的坐标与cos∠BAO的值;
(2)若A,O位置不变,将点B沿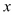 轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
相关试题

