【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20 ![]() 米.
米.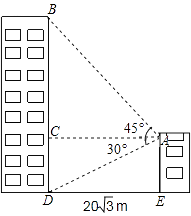
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
参考答案:
【答案】
(1)
解:如图,∵AC⊥BD,
∴BD⊥DE,AE⊥DE,
∴四边形AEDC是矩形,
∴AC=DE=20 ![]() 米,
米,
∵在Rt△ABC中,∠BAC=45°,
∴BC=AC=20 ![]() 米,
米,
在Rt△ACD中,tan30°= ![]() ,
,
∴CD=ACtan30°=20 ![]() ×
× ![]() =20(米),
=20(米),
∴BD=BC+CD=20 ![]() +20(米);
+20(米);
∴大厦的高度BD为:(20 ![]() +20)米
+20)米
(2)
解:∵四边形AEDC是矩形,
∴AE=CD=20米.
∴小敏家的高度AE为20米
【解析】(1)易得四边形AEDC是矩形,即可求得AC的长,然后分别在Rt△ABC与Rt△ACD中,利用三角函数的知识求得BC与CD的长,继而求得答案;(2)结合(1),由四边形AEDC是矩形,即可求得小敏家的高度AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某课题组为了解全市八年级学生对数学知识的掌握情况,在一次数学检测中,从全市24000名八年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
分数段
频数
频率
 <60
<6020
0.10
60≤
 <70
<7028
0.14
70≤
 <80
<8054
0.27
80≤
 <90
<90
0.20
90≤
 <100
<10024
0.12
100≤
 <110
<11018

110≤
 ≤120
≤12016
0.08

请根据以上图表提供的信息,解答下列问题:
(1)表中
 和
和 所表示的数分别为:
所表示的数分别为: = ,
= , = ;
= ;(2)请在图中,补全频数分布直方图;
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市24000名八年级考生数学成绩为优秀的学生约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
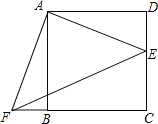
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A:体操,B:跑操,C:舞蹈,D:健美操四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:
(1)这次被调查的学生共有 人.
(2)请将统计图2补充完整.
(3)统计图1中B项目对应的扇形的圆心角是 度.
(4)已知该校共有学生3600人,请根据调查结果估计该校喜欢健美操的学生人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某采摘农场计划种植A,B两种草莓共6亩,根据表格信息,解答下列问题:
项目 品种
A
B
年亩产(单位:千克)
1200
2000
采摘价格
(单位:元/千克)60
40
(1)若该农场每年草莓全部被采摘的总收入为460000元,那么A、B两种草莓各种多少亩?
(2)若要求种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?并求出最多总收入. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
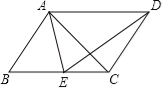
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段CB=6,点A在线段BC上,且CA=2,以AB为直径做半圆O,点D为半圆O上的动点,以CD为边向外作等边△CDE.
(1)发现:CD的最小值是 , 最大值是 , △CBD面积的最大值是 .
(2)思考:如图1,当线段CD所在直线与半圆O相切时,求弧BD的长.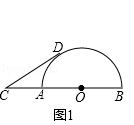
(3)探究:如图2,当线段CD与半圆O有两个公共点D,M时,若CM=DM,求等边△CDE面积.
相关试题

