【题目】如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
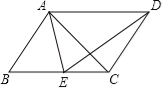
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
参考答案:
【答案】见解析
【解析】试题分析:从题中可知:(1)△ABC和△EAD中已经有一条边和一个角分别相等,根据平行的性质和等边对等角得出∠B=∠DAE即可证明.
(2)根据全等三角形的性质,利用平行四边形的性质求解即可.
(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∵在△ABC和△AED中,
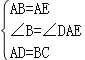 ,
,
∴△ABC≌△EAD.
(2)解:∵AE平分∠DAB(已知),
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=25°,
∴∠BAC=85°.
∵△ABC≌△EAD,
∴∠AED=∠BAC=85°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A:体操,B:跑操,C:舞蹈,D:健美操四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:
(1)这次被调查的学生共有 人.
(2)请将统计图2补充完整.
(3)统计图1中B项目对应的扇形的圆心角是 度.
(4)已知该校共有学生3600人,请根据调查结果估计该校喜欢健美操的学生人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20
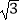 米.
米.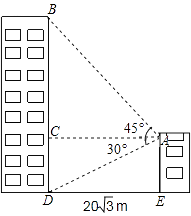
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE. -
科目: 来源: 题型:
查看答案和解析>>【题目】某采摘农场计划种植A,B两种草莓共6亩,根据表格信息,解答下列问题:
项目 品种
A
B
年亩产(单位:千克)
1200
2000
采摘价格
(单位:元/千克)60
40
(1)若该农场每年草莓全部被采摘的总收入为460000元,那么A、B两种草莓各种多少亩?
(2)若要求种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?并求出最多总收入. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段CB=6,点A在线段BC上,且CA=2,以AB为直径做半圆O,点D为半圆O上的动点,以CD为边向外作等边△CDE.
(1)发现:CD的最小值是 , 最大值是 , △CBD面积的最大值是 .
(2)思考:如图1,当线段CD所在直线与半圆O相切时,求弧BD的长.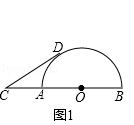
(3)探究:如图2,当线段CD与半圆O有两个公共点D,M时,若CM=DM,求等边△CDE面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2﹣2bx﹣3(b为常数,b<0).
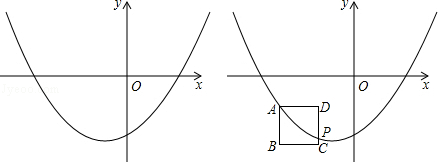
(1)抛物线y=x2﹣2bx﹣3总经过一定点,定点坐标为;
(2)抛物线的对称轴为直线x=(用含b的代数式表示),位于y轴的
侧.
(3)思考:若点P(﹣2,﹣1)在抛物线y=x2﹣2bx﹣3上,抛物线与反比例函数y=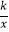 (k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(4)探究:设点A是抛物线上一点,且点A的横坐标为m,以点A为顶点做边长为1的正方形ABCD,AB⊥x轴,点C在点A的右下方,若抛物线与CD边相交于点P(不与D点重合且不在y轴上),点P的纵坐标为﹣3,求b与m之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )
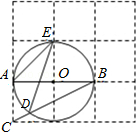
A.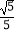
B.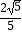
C.2
D.
相关试题

