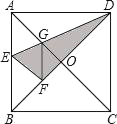
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:
①∠AGD=112.5°;②tan∠AED=![]() +1;③四边形AEFG是菱形;④S△ACD=
+1;③四边形AEFG是菱形;④S△ACD=![]() S△OCD.其中正确结论的序号是__.(把所有正确结论的序号都填在横线上)
S△OCD.其中正确结论的序号是__.(把所有正确结论的序号都填在横线上)
参考答案:
【答案】①②③
【解析】试题分析:∵四边形ABCD是正方形,
∴∠ADB=45°,
由折叠的性质可知,∠ADE=∠BDE=22.5°,
∴∠AGD=180°﹣90°﹣22.5°=112.5°,①正确;
设AE=x,
∵△BEF是等腰直角三角形,
∴BE=![]() EF=
EF=![]() AE=
AE=![]() x,
x,
∴x+![]() x=1,
x=1,
解得,x=![]() ﹣1,
﹣1,
∴tan∠AED=![]() =
=![]() +1,②正确;
+1,②正确;
由同位角相等可知,GF∥AB,EF∥AC,
∴四边形AEFG是平行四边形,
由折叠的性质可知,EA=EF,
∴四边形AEFG是菱形,③正确;
由正方形的性质可知,S△ACD=2S△OCD,④错误,
故答案为:①②③.
-
科目: 来源: 题型:
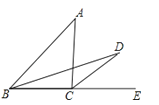
查看答案和解析>>【题目】如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
A.46°
B.92°
C.44°
D.23° -
科目: 来源: 题型:
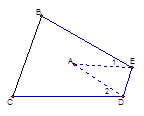
查看答案和解析>>【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2) -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,将点P(-3,2)向沿y轴方向向上平移4个单位长度后,得到的点坐标为( )
A. (-3,6) B. (1,2) C. (-7,2) D. (-3,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=50°,AD是BC边上的高,且∠DAC=20°,则∠BAC=°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算结果正确的是( )
A.(3x4)2=6x8
B.(﹣x4)3=﹣x12
C.(﹣4a3)2=4a6
D.〔(﹣a)4〕5=﹣a20 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4
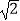 ,则四边形AECD的周长为( )
,则四边形AECD的周长为( ) 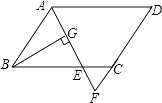
A.20
B.21
C.22
D.23
相关试题

