【题目】“如图1,在Rt△ABC中,∠ACB=90°,CD是△ABC的高,则△ACD与△CBD相似吗?”于是,学生甲发现CD2=AD·BD也成立.
问题1:请你证明CD2=AD·BD;

学生乙从CD2=AD·BD中得出:可以画出两条已知线段的比例中项.
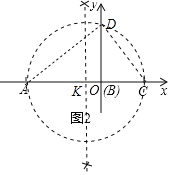
问题2:已知两条线段AB、BC在x轴上,如图2:请你用直尺(无刻度)和圆规作出这两条线段的比例中项.要求保留作图痕迹,不要写作法,最后指出所要作的线段.

学生丙也从CD2=AD·BD中悟出了矩形与正方形的等积作法.
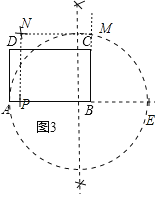
问题3:如图3,已知矩形ABCD,请你用直尺(无刻度)和圆规作出一个正方形BMNP,使得S正方形BMNP=S矩形ABCD.要求:保留作图痕迹;简要写出作图每个步骤的要点.

参考答案:
【答案】(1)证明见解析;(2)作图见解析,CD为所要画的线段;(3)过程见解析.
【解析】试题分析:问题1:只要证明△ACD∽△CBD,可得![]() ,即可证明;
,即可证明;
问题2:如图2中,作AC的中点K,以K为圆心KA为半径作⊙K交y轴正半轴于D.线段BD为所要画的线段;
问题3:①延长AB至E,使得BE=BC;②以AE为直径,画半圆O,与BC的延长线相交于M③以BM为边做正方形BMNP.正方形BMNP即为所求;
试题解析:问题1:证明:如图1中,
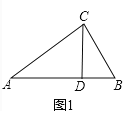
∵CD⊥AB,∠ACB=90°,
∴∠ADC=∠CDB=90°,
∴∠A+∠ACD=90°,∠A+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴![]() ,
,
∴CD2=ADBD.
问题2:如图2中,作AC的中点K,以K为圆心KA为半径作⊙K交y轴正半轴于D.
线段BD为所要画的线段。
问题3:①延长AB至E,使得BE=BC;
②以AE为直径,画半圆O,与BC的延长线相交于M
③以BM为边做正方形BMNP.
正方形BMNP即为所求。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,D为⊙O上一点,DE是⊙O的切线,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.

(1)求证:AD平分∠BAC;
(2)若DE=3,⊙O的半径为5,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AC、BD相交于点O,AE平分∠BAD,交BC于E,若∠EAO=15°,则∠BOE的度数为 度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
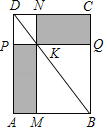
查看答案和解析>>【题目】如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2;(填“>”或“<”或“=”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明袋中装有红、黄、绿三种颜色的球共36个,它们除颜色外都相同,其中黄球个数是绿球个数的2倍,已知从袋中摸出一个球是红球的概率为
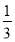 .
.(1)分别求红球和绿球的个数.
(2)求从袋中随机摸出一球是绿球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,
(1)问应将每件售价定为多少元时,才能使每天利润为640元且成本最少?
(2)问应将每件售价定为多少元时,才能使每天利润最大?
相关试题

