【题目】如图,矩形ABCD中,AC、BD相交于点O,AE平分∠BAD,交BC于E,若∠EAO=15°,则∠BOE的度数为 度.

参考答案:
【答案】75°.
【解析】
试题分析:根据矩形的性质可得△BOA为等边三角形,得出BA=BO,又因为△BAE为等腰直角三角形,BA=BE,由此关系可求出∠BOE的度数.
解:在矩形ABCD中,∵AE平分∠BAD,
∴∠BAE=∠EAD=45°,
又知∠EAO=15°,
∴∠OAB=60°,
∵OA=OB,
∴△BOA为等边三角形,
∴BA=BO,
∵∠BAE=45°,∠ABC=90°,
∴△BAE为等腰直角三角形,
∴BA=BE.
∴BE=BO,∠EBO=30°,
∠BOE=∠BEO,
此时∠BOE=75°.
故答案为75°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形( )
A. 三条中线的交点
B. 三条角平分线的交点
C. 三条边的垂直平分线的交点
D. 三条高的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的一边长为a+b,另一边长比这条边长b,第三边长比这条边短a-b(0<b<a).
(1)求这个三角形的周长(用含a、b的代数式表示);
(2)若a=5,b=3,求三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程a+x=5-(2a+1)x的解也是方程-x=x+2的解,则a的值是( )
A. -5 B. -6 C. -7 D. -8
-
科目: 来源: 题型:
查看答案和解析>>【题目】
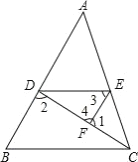
填空:
如图,已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠ACB.
证明:∵∠1+∠2=180°(已知)
∠1+________=180°(邻补角的定义)
∴∠2=________(同角的补角定义)
∴AB∥EF(___________________)
∴∠3=________(_____________________)
又∵∠3=∠B(已知)
∴∠B=________(等量代换)
∴DE∥BC(_________________)
∴∠AED=∠ACB(__________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.(10分)
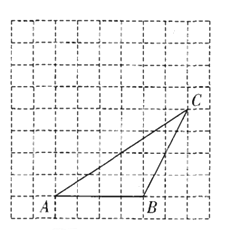
(1)请在图中画出平移后的△A′B′C′。
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是指大气中直径小于或等于0.000 002 5 m的颗粒物,将0.000 002 5用科学记数法表示为( )
A.
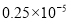 B.
B. 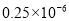 C.
C. 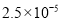 D.
D. 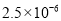
相关试题

