【题目】如图,AB为⊙O的直径,D为⊙O上一点,DE是⊙O的切线,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.

(1)求证:AD平分∠BAC;
(2)若DE=3,⊙O的半径为5,求BF的长.
参考答案:
【答案】(1)证明见解析;(2)BF=![]() .
.
【解析】
试题分析:(1)连接BC、OD,由D是弧BC的中点,可知:OD⊥BC;由OB为⊙O的直径,可得:BC⊥AC,根据DE⊥AC,可证OD⊥DE,从而可证DE是⊙O的切线;
(2)在Rt△ABC中,运用勾股定理可将爱那个AC的长求出,运用切割线定理可将AE的长求出,根据△AED∽△ABF,可将BF的长求出.
试题解析:(1)连接OD,BC,OD与BC相交于点G,

∵D是弧BC的中点,
∴OD垂直平分BC,
∵AB为⊙O的直径,
∴AC⊥BC,
∴OD∥AE.
∵DE⊥AC,
∴OD⊥DE,
∵OD为⊙O的半径,
∴DE是⊙O的切线.
(2)由(1)知:OD⊥BC,AC⊥BC,DE⊥AC,
∴四边形DECG为矩形,
∴CG=DE=3,
∴BC=6.
∵⊙O的半径为5,
∴AB=10,
∴AC=![]() =8,
=8,
由(1)知:DE为⊙O的切线,
∴DE2=ECEA,即32=(EA﹣8)EA,
解得:AE=9.
∵D为弧BC的中点,
∴∠EAD=∠FAB,
∵BF切⊙O于B,
∴∠FBA=90°.
又∵DE⊥AC于E,
∴∠E=90°,
∴∠FBA=∠E,
∴△AED∽△ABF,
∴![]() ,
,
∴BF=![]() .
.
考点:1.切线的判定,2.勾股定理,3.圆周角定理,4.相似三角形的判定与性质.
-
科目: 来源: 题型:
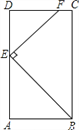
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,AD=6,点E在AD边上,且AE=4,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时 间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
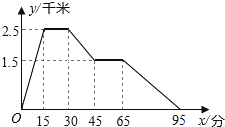
A. 体育场离张强家2.5千米
B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店1.千米
D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AC、BD相交于点O,AE平分∠BAD,交BC于E,若∠EAO=15°,则∠BOE的度数为 度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】“如图1,在Rt△ABC中,∠ACB=90°,CD是△ABC的高,则△ACD与△CBD相似吗?”于是,学生甲发现CD2=AD·BD也成立.
问题1:请你证明CD2=AD·BD;

学生乙从CD2=AD·BD中得出:可以画出两条已知线段的比例中项.
问题2:已知两条线段AB、BC在x轴上,如图2:请你用直尺(无刻度)和圆规作出这两条线段的比例中项.要求保留作图痕迹,不要写作法,最后指出所要作的线段.

学生丙也从CD2=AD·BD中悟出了矩形与正方形的等积作法.
问题3:如图3,已知矩形ABCD,请你用直尺(无刻度)和圆规作出一个正方形BMNP,使得S正方形BMNP=S矩形ABCD.要求:保留作图痕迹;简要写出作图每个步骤的要点.

相关试题

