搜索
【题目】如图，AB⊥y轴，垂足为B，将△ABO绕点A逆时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y=﹣ 
x上，再将△AB1O1绕点B1逆时针旋转到△A1B1O1的位置，使点O1的对应点O2落在直线y=﹣ x上，依次进行下去…若点B的坐标是（0，1），则点O12的纵坐标为 ．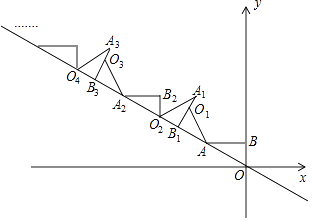 
参考答案：
【答案】（﹣9﹣9 
，9+3 ）
【解析】解：观察图象可知，O12在直线y=﹣ 
x时， OO12=6OO2=6（1+ +2）=18+6 ，
∴O12的横坐标=﹣（18+6 ）cos30°=﹣9﹣9 ，
O12的纵坐标= 
OO12=9+3 ，
∴O12（﹣9﹣9 ，9+3 ）．
所以答案是（﹣9﹣9 ，9+3 ）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，A（1，2），B（3，1），C（﹣2，﹣1）．
（1）在图中作出△ABC 关于 y 轴对称的△A1B1C1．
（2）△A1B1C1 的面积为___________．
（3）在 x 轴上找出一点P，使PA+PB的值最小直接画出点P的位置．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y=ax+b和反比例函数y=
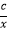在同一平面直角坐标系中的图象如图所示，则二次函数y=ax2+bx+c的图象可能是（ ）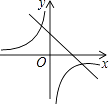 
A.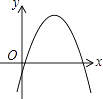
B.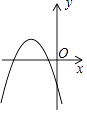
C.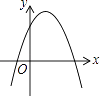
D.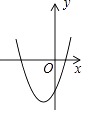
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A、D、F、B在同一直线上，AD＝BF，AE＝BC，且AE∥BC．
求证：（1）EF＝CD；（2）EF∥CD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（题文）(1)阅读理解：
如图1，在△ABC中，若AB＝10，AC＝6，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE＝AD，连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD，把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是_________；
(2)问题解决：
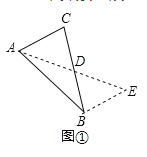
如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证BE＋CF＞EF.
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：﹣12﹣|3﹣
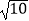|+2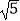 
sin45°﹣（ 
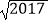﹣1）2 ． -
科目： 来源： 题型：
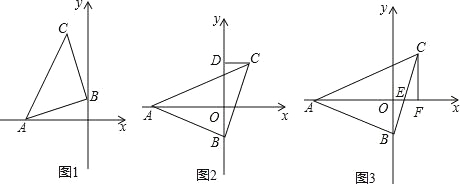
查看答案和解析>>【题目】已知，△ABC 是等腰直角三角形，BC=AB，A 点在 x 负半轴上，直角顶点 B 在 y 轴上，点 C 在 x 轴上方．
（1）如图1所示，若A的坐标是（﹣3，0），点 B的坐标是（0，1），求点 C 的坐标；
（2）如图2，过点 C 作 CD⊥y 轴于 D，请直接写出线段OA，OD，CD之间等量关系；
（3）如图3，若 x 轴恰好平分∠BAC，BC与 x 轴交于点 E，过点 C作 CF⊥x 轴于 F，问 CF 与 AE 有怎样的数量关系？并说明理由．
相关试题
