搜索
【题目】计算：﹣12﹣|3﹣ 
|+2 
sin45°﹣（ 
﹣1）2 ．
参考答案：
【答案】解：原式=﹣1﹣（ 
﹣3）+2 
× 
﹣（2017+1﹣2 
） =﹣1+3﹣ + ﹣2018+2
=﹣2016+2
【解析】直接利用绝对值的性质以及特殊角的三角函数值和完全平方公式分别化简求出答案．
【考点精析】关于本题考查的二次根式的混合运算和特殊角的三角函数值，需要了解二次根式的混合运算与实数中的运算顺序一样，先乘方，再乘除，最后加减，有括号的先算括号里的（或先去括号）；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A、D、F、B在同一直线上，AD＝BF，AE＝BC，且AE∥BC．
求证：（1）EF＝CD；（2）EF∥CD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB⊥y轴，垂足为B，将△ABO绕点A逆时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y=﹣
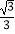x上，再将△AB1O1绕点B1逆时针旋转到△A1B1O1的位置，使点O1的对应点O2落在直线y=﹣ 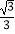x上，依次进行下去…若点B的坐标是（0，1），则点O12的纵坐标为 ．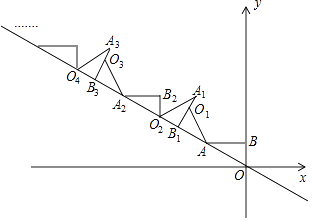 
-
科目： 来源： 题型：
查看答案和解析>>【题目】（题文）(1)阅读理解：
如图1，在△ABC中，若AB＝10，AC＝6，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE＝AD，连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD，把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是_________；
(2)问题解决：
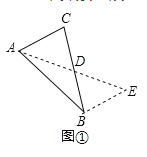
如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证BE＋CF＞EF.
-
科目： 来源： 题型：
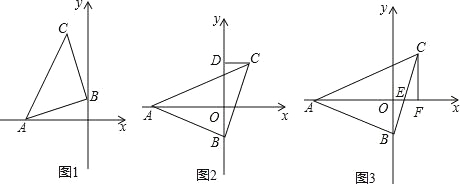
查看答案和解析>>【题目】已知，△ABC 是等腰直角三角形，BC=AB，A 点在 x 负半轴上，直角顶点 B 在 y 轴上，点 C 在 x 轴上方．
（1）如图1所示，若A的坐标是（﹣3，0），点 B的坐标是（0，1），求点 C 的坐标；
（2）如图2，过点 C 作 CD⊥y 轴于 D，请直接写出线段OA，OD，CD之间等量关系；
（3）如图3，若 x 轴恰好平分∠BAC，BC与 x 轴交于点 E，过点 C作 CF⊥x 轴于 F，问 CF 与 AE 有怎样的数量关系？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．
（1）求证：△ABQ≌△CAP；
（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．
（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，直接写出它的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化，两位采购员的购货方式也不同，其中，甲每次购买1000千克，乙每次用去800元，而不管购买多少饲料.
（1）甲、乙所购饲料的平均单价各是多少？
（2）谁的购货方式更合算？
相关试题
