【题目】(题文)(1)阅读理解:
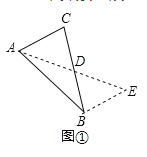
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:

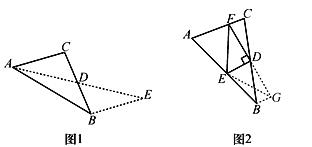
如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
参考答案:
【答案】(1)2<AD<8(2)证明见解析
【解析】试题分析:(1)延长AD到E,使AD=DE,连接BE,△ADC≌△EDB,推出EB=AC,根据三角形的三边关系求出即可;
(2)先利用ASA判定△BGD≌△CFD,从而得出BG=CF;再利用全等的性质可得GD=FD,BG=CF,再有DE⊥DF,从而得出EG=EF,两边和大于第三边从而得出BE+CF>EF.
试题解析:(1)延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,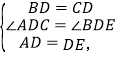
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系得:ABAC<AE<AC+AB,
∴4<AE<16,
∵AE=2AD
∴2<AD<8,
即:BC边上的中线AD的取值范围2<AD<8;
故答案为:2<AD<8.
(2)BE+CF>EF.
理由:如图2,
过点B作![]() 交FD的延长线于G,
交FD的延长线于G,
∴∠DBG=∠DCF.
∵D为BC的中点,
∴BD=CD
又∵∠BDG=∠CDF,
在△BGD与△CFD中,
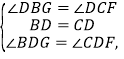
∴△BGD≌△CFD(ASA).
∴GD=FD,BG=CF.
又∵DE⊥DF,
∴EG=EF(垂直平分线到线段端点的距离相等).
∴在△EBG中,BE+BG>EG,
即BE+CF>EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图E在△ABC的边AC上,且∠AEB=∠ABC.
⑴求证:∠ABE=∠C;
⑵若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
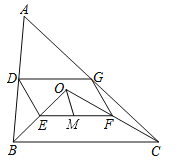
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(x﹣3,x+3)是x轴上一点,则点P的坐标是( )
A.(0,6)B.(0,﹣6)C.(﹣6,0)D.(6,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把点A(3,5)向下平移3个单位长度,再向左平移2个单位长度后,得对应点A1的坐标是( )
A.(1,2)B.(2,1)C.(﹣1,2)D.(﹣1,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果教室里座位号(5,3)表示第5列第3排,则座位号(3,5)表示_____.
相关试题

