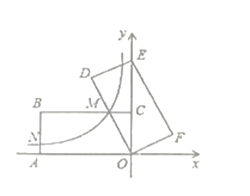
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的负半轴、
轴的负半轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限.将矩形
在第二象限.将矩形![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在
落在![]() 轴上,得到矩形
轴上,得到矩形![]() 与
与![]() 相交于点
相交于点![]() .若经过点
.若经过点![]() 的反比例函数
的反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() 的图象交
的图象交![]() 于点
于点![]()
![]() 则
则![]() 的长为____.
的长为____.
参考答案:
【答案】![]()
【解析】
利用矩形的面积公式得到ABBC=32,再根据旋转的性质得AB=DE,OD=OA,接着利用正切的定义得到tan∠DOE=![]() ,所以DE2DE=32,解得DE=4,于是得到AB=4,OA=8,同样在Rt△OCM中利用正切定义得到MC=2,则M(2,4),易得反比例函数解析式为y=
,所以DE2DE=32,解得DE=4,于是得到AB=4,OA=8,同样在Rt△OCM中利用正切定义得到MC=2,则M(2,4),易得反比例函数解析式为y=![]() ,然后确定N点坐标,最后计算BN的长.
,然后确定N点坐标,最后计算BN的长.
解:∵S矩形OABC=32,
∴ABBC=32,
∵矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,
∴AB=DE,OD=OA,
在Rt△ODE中,tan∠DOE=![]() ,即OD=2DE,
,即OD=2DE,
∴DE2DE=32,解得DE=4,
∴AB=4,OA=8,
在Rt△OCM中,∵tan∠COM=![]() ,
,
而OC=AB=4,
∴MC=2,
∴M(2,4),
把M(2,4)代入![]() 中,得k=2×4=8,
中,得k=2×4=8,
∴反比例函数解析式为y=![]() ,
,
当x=8时,y=1,
则N(8,1),
∴BN=41=3.
故答案为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题为真命题的是( )
A.两组身高数据的方差分别是
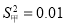 ,
,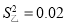 ,那么乙组的身高比较整齐
,那么乙组的身高比较整齐B.“明天下雨”是必然事件
C.一组数据3,5,4,5,6,7的众数、中位数和平均数都是5
D.为了解某灯管的使用寿命,可以采用普查的方式进行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以
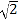 cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC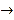 CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
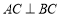 ,
,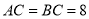 ,以
,以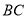 为直径作半圆,圆心为点
为直径作半圆,圆心为点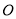 ;以点
;以点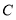 为圆心,
为圆心,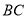 为半径作
为半径作 ,过点
,过点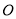 作
作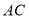 的平行线交两弧于点
的平行线交两弧于点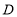 、
、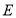 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )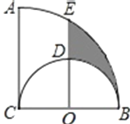
A.
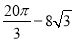 B.
B.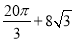 C.
C.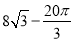 D.
D.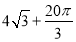
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案.
-
科目: 来源: 题型:
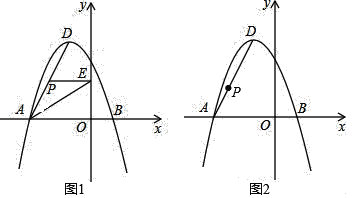
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;
(3)如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
相关试题

