【题目】如图,已知AC=BC=CD,BD平分∠ABC,点E在BC的延长线上.

(1)试说明CD∥AB的理由;
(2)CD是∠ACE的角平分线吗?为什么?
参考答案:
【答案】(1)理由见解析;(2)CD是∠ACE的角平分线,理由见解析;
【解析】
(1)由BD平分∠ABC,可得∠ABD=∠DBC,而BC=CD,可得∠DBC=∠D,从而可得∠ABD=∠D,从而可证CD∥AB;
(2)CD是∠ACE的角平分线,由于CD∥AB,可知∠DCE=∠ABE,∠ACD=∠A,而AC=BC,易得∠A=∠ABE,等量代换可证∠ACD=∠DCE,从而可知CD是∠ACE的角平分线.
解:(1)∵BD平分∠ABC(已知),
∴∠ABD=∠DBC(角平分线定义),
∵BC=CD(已知),
∴∠DBC=∠D(等边对等角),
∴∠ABD=∠D(等量代换),
∴CD∥AB(内错角相等,两直线平行);
(2)CD是∠ACE的角平分线.理由如下:
∵CD∥AB,
∴∠DCE=∠ABE(两直线平行,同位角相等),∠ACD=∠A(两直线平行,内错角相等),∵AC=BC(已知),
∴∠A=∠ABE(等边对等角),
∴∠ACD=∠DCE(等量代换),即CD是∠ACE的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用棋子按下面的规律摆图形,则摆第2018个图形需要围棋子( )枚.

A. 6053B. 6054C. 6056D. 6060
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
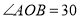 °,点
°,点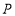 在
在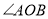 的内部,点
的内部,点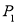 与点
与点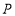 关于
关于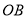 对称,点
对称,点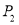 与点
与点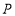 关于
关于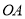 对称,若
对称,若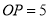 ,则
,则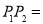 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=
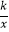 (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.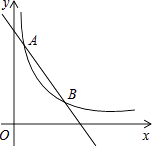
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年4月20日19点41分,天舟一号由长征七号火箭发生升空,经过一天多的飞行,4月22日中午,天舟一号与天宫二号空间实验室进行自动交会对接,形成组合体,某商家根据市场预测,购进“天舟一号”(记作A)、“天宫二号”(记作B)两种航天模型,若购进A种模型10件,B种模型5件,需要1000元;若购进A种模型4件,B种模型3件,需要550元.
(1)求购进A,B两种模型每件需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种模型,考虑到市场需求,要求购进A种模型的数量不超过B种模型数量的8倍,且B种模型最多购进33件,那么该商店共有几种进货方案?
(3)若销售每件A种模型可获利润20元,每件B种模型可获利润30元,在第(2)问的前提下,设销售总盈利为W元,购买B种模型m件,请求出W关于x的函数关系式,并求出当m为何值时,销售总盈利最大,并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,已知点
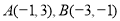 ,将点
,将点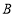 向右平移5个单位得到点
向右平移5个单位得到点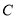
(1)描出点
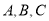 的位置,并求
的位置,并求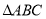 的面积.
的面积.(2)若在
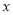 轴下方有一点
轴下方有一点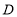 ,使
,使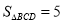 ,写出一个满足条件的点
,写出一个满足条件的点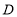 的坐标.并指出满足条件的点
的坐标.并指出满足条件的点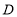 有什么特征.
有什么特征.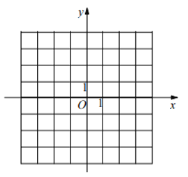
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求回答问题:
(1)【提出问题】
已知:菱形ABCD的变长为4,∠ADC=60°,△PEF为等边三角形,当点P与点D重合,点E在对角线AC上时(如图1所示),求AE+AF的值;
(2)【类比探究】
在上面的问题中,如果把点P沿DA方向移动,使PD=1,其余条件不变(如图2),你能发现AE+AF的值是多少?请直接写出你的结论;
(3)【拓展迁移】
在原问题中,当点P在线段DA的延长线上,点E在CA的延长线上时(如图3),设AP=m,则线段AE、AF的长与m有怎样的数量关系?请说明理由.
相关试题

