【题目】根据要求回答问题:
(1)【提出问题】
已知:菱形ABCD的变长为4,∠ADC=60°,△PEF为等边三角形,当点P与点D重合,点E在对角线AC上时(如图1所示),求AE+AF的值;
(2)【类比探究】
在上面的问题中,如果把点P沿DA方向移动,使PD=1,其余条件不变(如图2),你能发现AE+AF的值是多少?请直接写出你的结论;
(3)【拓展迁移】
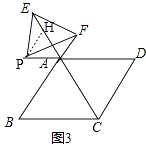
在原问题中,当点P在线段DA的延长线上,点E在CA的延长线上时(如图3),设AP=m,则线段AE、AF的长与m有怎样的数量关系?请说明理由.
参考答案:
【答案】
(1)解:如图1,
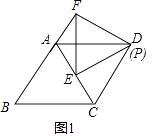 ,
,
∵四边形ABCD是菱形,
∴PA=PC,
∵∠ADC=60°,
∴△ACD是等边三角形,
∴AC=AD=4,
又∵△PEF为等边三角形,
∴∠ADC=∠EPF=60°,
∴∠APF=∠CPE,
在△APF和△CPE中,
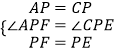
∴△APF≌△CPE,
∴CE=AF,
∴AE+AF=AE+CE=AC=4,
即AE+AF的值是4.
(2)解:如图2,点G是AC上的一点,且满足CG=PD=1,
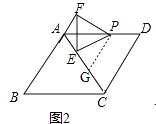 ,
,
∵CG=PD,AC=AD,
∴AG=AP,
∴ ![]() ,
,
∴GP∥CD,
∴∠GPA=∠CDA=60°,
又∵EPF=60°,
∴∠APF=∠GPE,
在△APF和△GPE中,
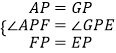
∴△APF≌△GPE,
∴GE=AF,
∴AE+AF=AE+GE=AG=AC﹣CG=4﹣1=3,
即AE+AF的值是3
(3)解:如图3,作PH∥CD交CE于点H,
 ,
,
由(1),可得△ACD是等边三角形,
∵PH∥CD,
∴△AHP∽△ACD,
∴△AHP是等边三角形,
∴PA=PH,∠APH=∠EPF=60°,
∴∠FPA=∠EPH,
在△APF和△HPE中,
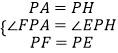
∴△APF≌△HPE,
∴AF=HE,
又∵PA=AH,
∴AE=PA+AF,
∴AE﹣AF=m.
【解析】(1)首先判断出△ACD是等边三角形,即可判断出AC=AD=4;然后根据全等三角形判定的方法,判断出△APF≌△CPE,即可判断出CE=AF,据此求出AE+AF的值是多少即可.(2)首先取AC上的点G,使得CG=PD=1,判断出GP∥CD,即可判断出∠APF=∠GPE;然后根据全等三角形判定的方法,判断出△APF≌△GPE,即可判断出GE=AF,据此求出AE+AF的值是多少即可.(3)首先作PH∥CD交CE于点H,判断出△AHP∽△ACD,即可判断出△AHP是等边三角形;然后根据全等三角形判定的方法,判断出△APF≌△HPE,即可判断出AF=HE,再根据PA=AH,可得AE=PA+AF,所以AE﹣AF=m,据此解答即可.
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC=BC=CD,BD平分∠ABC,点E在BC的延长线上.

(1)试说明CD∥AB的理由;
(2)CD是∠ACE的角平分线吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年4月20日19点41分,天舟一号由长征七号火箭发生升空,经过一天多的飞行,4月22日中午,天舟一号与天宫二号空间实验室进行自动交会对接,形成组合体,某商家根据市场预测,购进“天舟一号”(记作A)、“天宫二号”(记作B)两种航天模型,若购进A种模型10件,B种模型5件,需要1000元;若购进A种模型4件,B种模型3件,需要550元.
(1)求购进A,B两种模型每件需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种模型,考虑到市场需求,要求购进A种模型的数量不超过B种模型数量的8倍,且B种模型最多购进33件,那么该商店共有几种进货方案?
(3)若销售每件A种模型可获利润20元,每件B种模型可获利润30元,在第(2)问的前提下,设销售总盈利为W元,购买B种模型m件,请求出W关于x的函数关系式,并求出当m为何值时,销售总盈利最大,并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,已知点
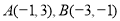 ,将点
,将点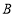 向右平移5个单位得到点
向右平移5个单位得到点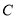
(1)描出点
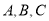 的位置,并求
的位置,并求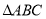 的面积.
的面积.(2)若在
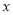 轴下方有一点
轴下方有一点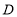 ,使
,使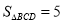 ,写出一个满足条件的点
,写出一个满足条件的点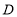 的坐标.并指出满足条件的点
的坐标.并指出满足条件的点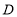 有什么特征.
有什么特征.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
颜色
红
黄
蓝
白
紫
绿
花朵数
1
2
3
4
5
6
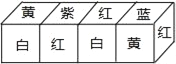
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如图所示,那么长方体的下底面共有_____朵花.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,点D,E分别在AC,BC上,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若PF=2,则BP=( )

A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A
 B
B C
C ;
;(2) 请画出△ABC关于原点对称的△A
 B
B C
C ;
;(3) 在
 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
相关试题

