【题目】从长度分别为3,5,6,9的四条线段中任取三条,能组成三角形的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:从长度分别为3,5,6,9的四条线段中任取三条的所有可能性是: (3,5,6)、(3,5,9)、(3,6,9)、(5,6,9),
能组成三角形的可能性是:(3,5,6)、(5,6,9),
∴能组成三角形的概率为: ![]() ,
,
故选D.
【考点精析】认真审题,首先需要了解三角形三边关系(三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边),还要掌握列表法与树状图法(当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DBEC.(填“>”,“<”或“=”)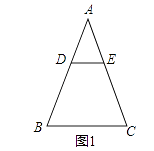
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.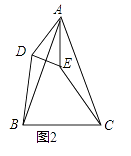
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.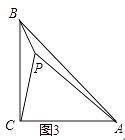
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1抛物线y=ax2+bx+c过 A(﹣1,0)、B(4,0)、C(0,2)三点.
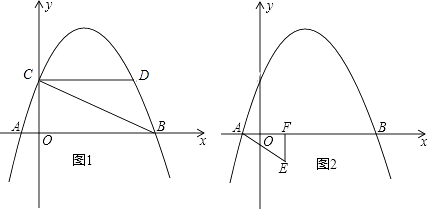
(1)求抛物线解析式;
(2)点C,D关于抛物线对称轴对称,求△BCD的面积;
(3)如图2,过点E(1,﹣1)作EF⊥x轴于点F,将△AEF绕平面内某点旋转180°得△MNQ(点M、N、Q分别与A、E、F对应)使得M、N在抛物线上,求M、N的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论:①b2﹣4ac>0;②a>0;③b>0;④c>0;⑤4a+2b+c<0,则其中结论正确的个数是( )

A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】利用直尺和圆规作一个角等于已知角的作法如下:
①以点O为圆心,以任意长为半径画弧,分别交OA、OB于点D、C;
②作射线O′B′,以点O′为圆心,以 长为半径画弧,交O′B′于点C′;
③以点C′为圆心,以 长为半径画弧,两弧交于点D′;
④过点D′作射线O′A′,∴∠A′O′B′为所求.
(1)请将上面的作法补充完整;
(2)△OCD≌△O′C′D′的依据是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

相关试题

