搜索
【题目】如图，在ABCD中，E为BC边上一点，且AB＝AE．
（1）求证：△ABC≌△EAD；
（2）若∠B＝65°，∠EAC＝25°，求∠AED的度数．
参考答案：
【答案】（1）见解析；（2）∠AED＝75°．
【解析】
（1）先证明∠B＝∠EAD，然后利用SAS可进行全等的证明；
（2）先根据等腰三角形的性质可得∠BAE＝50°，求出∠BAC的度数，即可得∠AED的度数．
（1）证明：∵在平行四边形ABCD中，AD∥BC，BC＝AD，
∴∠EAD＝∠AEB，
又∵AB＝AE，
∴∠B＝∠AEB，
∴∠B＝∠EAD，
在△ABC和△EAD中，
，
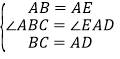∴△ABC≌△EAD（SAS）．
（2）解：∵AB＝AE，
∴∠B＝∠AEB，
∴∠BAE＝50°，
∴∠BAC＝∠BAE+∠EAC＝50°+25°＝75°，
∵△ABC≌△EAD，
∴∠AED＝∠BAC＝75°．
-
科目： 来源： 题型：
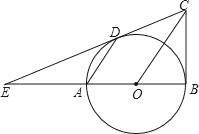
查看答案和解析>>【题目】如图所示，已知AB是⊙O的直径，BC⊥AB，连接OC，弦AD∥OC，直线CD交BA的延长线于点E．
（1）求证：直线CD是⊙O的切线；
（2）若DE=2BC，求AD：OC的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）阅读下文，寻找规律：
已知 x≠1 时，（1－x)（1＋x)＝1－x
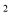，(1－x)(1＋x＋x
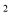)＝1－x
，(1－x)(1＋x＋x
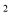＋x)＝1－x
.…观察上式，并猜想：
(1－x)(1＋x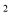＋x
＋ x＋x)＝ ____________. (1－x)(1＋x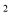＋x＋…＋x
)＝ ____________.（2） 通过以上规律，请你进行下面的探素：
①(a－b)(a＋b)＝ ____________.
②(a－b)(a
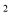＋ab＋b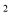)＝ ____________.③(a－b)(a
＋a
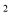＋ab＋b )＝ ____________.（3） 根据你的猜想，计算：
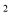1＋2＋2
＋…＋2
＋2
＋2
-
科目： 来源： 题型：
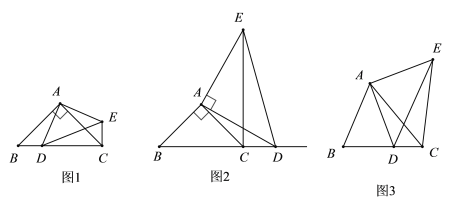
查看答案和解析>>【题目】如图，在△ABC中，∠ABC为锐角，点D为直线BC上一动点，以AD为直角边且在AD的右侧作等腰直角三角形ADE，∠DAE＝90°，AD＝AE．
（1）如果AB＝AC，∠BAC＝90°．①当点D在线段BC上时，如图1，线段CE、BD的位置关系为___________，数量关系为___________
②当点D在线段BC的延长线上时，如图2，①中的结论是否仍然成立，请说明理由．
（2）如图3，如果AB≠AC，∠BAC≠90°，点D在线段BC上运动。探究：当∠ACB多少度时，CE⊥BC？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图小方格的边长为1个单位。
(1)画出坐标系，使A、B的坐标分别为(1,1)、(-2,0)，并写出点C的坐标；
(2)若将△ABC向右平移4个单位，再向上平移3个单位，得到
，在图中画出；(3)写出△ABC的面积.
-
科目： 来源： 题型：
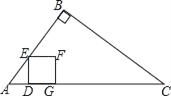
查看答案和解析>>【题目】如图，在Rt△ABC中，∠B=90°，AB=6cm，BC=8cm，点D从点A出发以1cm/s的速度运动到点C停止．作DE⊥AC交边AB或BC于点E，以DE为边向右作正方形DEFG．设点D的运动时间为t（s）．
（1）求AC的长．
（2）请用含t的代数式表示线段DE的长．
（3）当点F在边BC上时，求t的值．
（4）设正方形DEFG与△ABC重叠部分图形的面积为S（cm2），当重叠部分图形为四边形时，求S与t之间的函数关系式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛(斛是古代的一种容量位)，1个大桶加上5个小桶可以盛酒2斛。
(1)1个大桶、1个小桶分别可以盛酒多少斛？
(2)盛酒16斛，需要大桶、小桶各多少？(写出两种方案即可)
相关试题
