【题目】为了解青少年形体情况,现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题: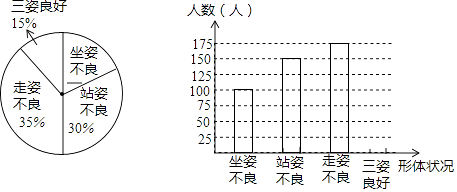
(1)求这次被抽查形体测评的学生一共有多少人?
(2)求在被调查的学生中三姿良好的学生人数,并将条形统计图补充完整;
(3)若全市有5万名初中生,那么估计全市初中生中,坐姿和站姿不良的学生共有多少人?
参考答案:
【答案】
(1)解:100÷20%=500(名),
答:这次被抽查形体测评的学生一共是500名;
(2)解:三姿良好的学生人数:500×15%=75名,
补全统计图如图所示; 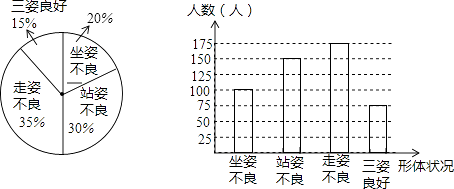
(3)解:5万×(20%+30%)=2.5万,
答:全市初中生中,坐姿和站姿不良的学生有2.5万人.
【解析】(1)观察扇形统计图和条形统计图,列式计算即可。
(2)先根据各部分所占的百分比的和等于1,求出坐姿不良所占的百分比,然后抽查学生的总数,求出三姿良好的学生人数,最后补全统计图即可。
(3)用全市初中生总人数乘以坐姿和站姿不良的学生的百分比之和,列式计算即可求解。
【考点精析】解答此题的关键在于理解扇形统计图的相关知识,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况,以及对条形统计图的理解,了解能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AD是BC边上的中线,有以下结论:①AD平分∠BAC;②△ABD的周长-△ACD的周长=AB-AC;③BC=2AD;④△ABD的面积是△ABC面积的一半.其中正确的是( )

A.①②④B.②③④C.②④D.③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
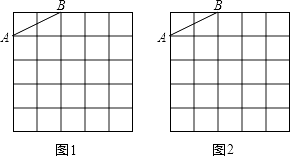
(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)

(2)(15x4y2-12x2y3-3x2)÷(-3x2)
(3)

(4)〔(x+y)2-(x-y) 2〕÷2xy
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。

(1)这个梯子的顶端离地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
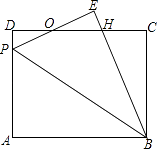
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想
 的最小值为多少?
的最小值为多少?
相关试题

