【题目】图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.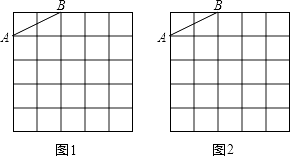
(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3.
参考答案:
【答案】
(1)解:如图1所示:△ABC即为所求,
△ABC的周长为: ![]() +2
+2 ![]() +5=5+3
+5=5+3 ![]() ;
;
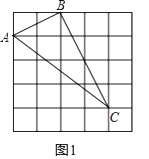
(2)解:如图2所示:△ABD中,∠ADB=45°,且面积为3.
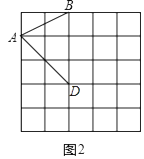
【解析】(1)直接利用勾股定理,结合网格中线段AB的长,得出符合题意得图形,再根据勾股定理求出其边长,即可求出周长。
(2)直接利用直角三角形的面积的求法,结合网格就可以确定点D的位置。。
【考点精析】关于本题考查的勾股定理的概念,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中(非矩形),连接AC,△ABC为直角三角形,若AB=4,AC=3,则AD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=
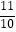 ,则tan∠BAD= .
,则tan∠BAD= . 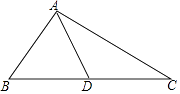
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AD是BC边上的中线,有以下结论:①AD平分∠BAC;②△ABD的周长-△ACD的周长=AB-AC;③BC=2AD;④△ABD的面积是△ABC面积的一半.其中正确的是( )

A.①②④B.②③④C.②④D.③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)

(2)(15x4y2-12x2y3-3x2)÷(-3x2)
(3)

(4)〔(x+y)2-(x-y) 2〕÷2xy
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解青少年形体情况,现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
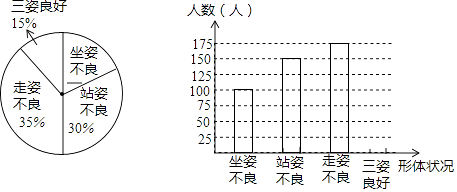
(1)求这次被抽查形体测评的学生一共有多少人?
(2)求在被调查的学生中三姿良好的学生人数,并将条形统计图补充完整;
(3)若全市有5万名初中生,那么估计全市初中生中,坐姿和站姿不良的学生共有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。

(1)这个梯子的顶端离地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
相关试题

