【题目】如图,已知![]() 两地相距6千米,甲骑自行车从
两地相距6千米,甲骑自行车从![]() 地出发前往
地出发前往![]() 地,同时乙从
地,同时乙从![]() 地出发步行前往
地出发步行前往![]() 地.
地.

(1)已知甲的速度为16千米/小时,乙的速度为4千米/小时,求两人出发几小时后甲追上乙;
(2)甲追上乙后,两人都提高了速度,但甲比乙每小时仍然多行12千米,甲到达![]() 地后立即返回,两人在
地后立即返回,两人在![]() 两地的中点处相遇,此时离甲追上乙又经过了2小时.求
两地的中点处相遇,此时离甲追上乙又经过了2小时.求![]() 两地相距多少千米.
两地相距多少千米.
参考答案:
【答案】(1)两人出发![]() 小时后甲追上乙;(2)
小时后甲追上乙;(2)![]() 两地相距30千米.
两地相距30千米.
【解析】
(1)设两人出发t小时后甲追上乙,根据题意就有16t﹣4t=6,解方程即可求解;
(2)可设速度提高了a千米/小时,BC段长度为x千米,两人在B、C两地的中点处相遇,则甲比乙多走的路程为BC段,于是可得方程2(16+a)﹣2(4+a)=x,解方程即可得BC段,于是可求A、C两地距离.
(1)设两人出发t小时后甲追上乙,根据题意得
16t﹣4t=6,
得t=![]() ,
,
答:两人出发![]() 小时后甲追上乙;
小时后甲追上乙;
(2)设两个人的速度提高了a千米/小时,BC段长度为x千米,根据题意有
2(16+a)﹣2(4+a)=x,
得x=24,
故BC段距离为24千米,
∴AC=AB+BC=6+24=30,
答:A、C两地相距30千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角板
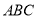 和直角三角板
和直角三角板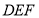 ,
,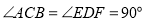 ,
,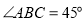 ,
,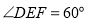 .
.(1)如图1,将顶点
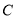 和顶点
和顶点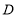 重合,保持三角板
重合,保持三角板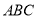 不动,将三角板
不动,将三角板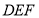 绕点
绕点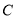 旋转.当
旋转.当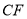 平分
平分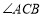 时,求
时,求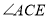 的度数;
的度数;(2)在(1)的条件下,继续旋转三角板
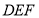 ,猜想
,猜想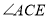 与
与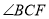 有怎样的数量关系?并利用图2所给的情形说明理由;
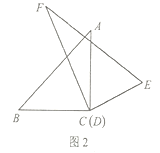
有怎样的数量关系?并利用图2所给的情形说明理由;(3)如图3,将顶点
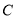 和顶点
和顶点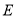 重合,保持三角板
重合,保持三角板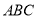 不动,将三角板
不动,将三角板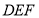 绕点
绕点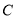 旋转.当
旋转.当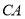 落在
落在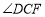 内部时,直接写出
内部时,直接写出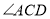 与
与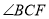 的数量关系.
的数量关系.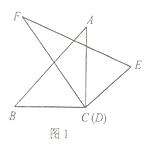
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=
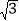 MN.
MN.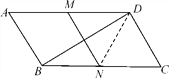
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第1个等式:
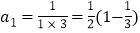
第2个等式:
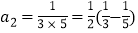
第3等式:
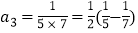
第4个等式:
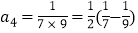
请解答下列问题:
(1)按以上规律写出第5个等式:a5= = .
(2)用含n的式子表示第n个等式:an= = (n为正整数).
(3)求a1+a2+a3+a4+…+a2018的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明,如图点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
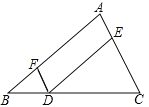
证明:∵DE∥AB,
∴∠FDE=∠ ( )
∵DF∥CA,
∴∠A=∠ ( )
∴∠FDE=∠A( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

相关试题

