【题目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,
![]() .
.
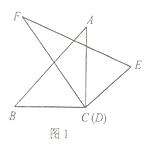
(1)如图1,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 平分
平分![]() 时,求
时,求![]() 的度数;
的度数;
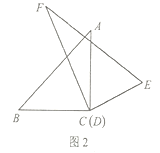
(2)在(1)的条件下,继续旋转三角板![]() ,猜想
,猜想![]() 与
与![]() 有怎样的数量关系?并利用图2所给的情形说明理由;
有怎样的数量关系?并利用图2所给的情形说明理由;
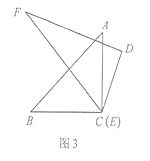
(3)如图3,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 落在
落在![]() 内部时,直接写出
内部时,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() , 理由见解析;(3)
, 理由见解析;(3)![]() .
.
【解析】
(1)利用角平分线的定义求出∠ACF=45°,然后利用余角的性质求解即可;
(2)依据同角的余角相等即可求解;
(3)∠ACD与∠BCF都与∠ACF关系紧密,分别表示它们与∠ACF的关系即可求解.
(1)∵CF是∠ACB的平分线,∠ACB=90°,
∴∠ACF=90°÷2=45°,
又∵∠FCE=90°,
∴∠ACE=∠FCE﹣∠ACF=90°﹣45°=45°;
(2)∵∠BCF+∠ACF=90°,
∠ACE+∠ACF=90°,
∴∠BCF=∠ACE;
(3)∵∠FCA=∠FCD﹣∠ACD=60°﹣∠ACD,
∠FCA=∠ACB﹣∠BCF=90°﹣∠BCF,
∴60°﹣∠ACD=90°﹣∠BCF,
∠ACD=30°﹣∠BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是菱形ABCD的对角线AC上一动点,过P作垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( )

A.
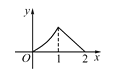 B.
B. 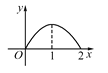
C.
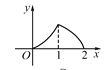 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1所示的三棱柱,高为
 ,底面是一个边长为
,底面是一个边长为 的等边三角形.
的等边三角形.(1)这个三棱柱有 条棱,有 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 条棱,需剪开棱的棱长的和的最大值为
 .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )

A. 4 B.
 C.
C.  D. 30
D. 30 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=
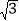 MN.
MN.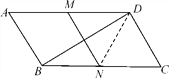
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 两地相距6千米,甲骑自行车从
两地相距6千米,甲骑自行车从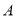 地出发前往
地出发前往 地,同时乙从
地,同时乙从 地出发步行前往
地出发步行前往 地.
地.
(1)已知甲的速度为16千米/小时,乙的速度为4千米/小时,求两人出发几小时后甲追上乙;
(2)甲追上乙后,两人都提高了速度,但甲比乙每小时仍然多行12千米,甲到达
 地后立即返回,两人在
地后立即返回,两人在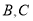 两地的中点处相遇,此时离甲追上乙又经过了2小时.求
两地的中点处相遇,此时离甲追上乙又经过了2小时.求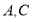 两地相距多少千米.
两地相距多少千米.
相关试题

