搜索
【题目】完成下面的证明，如图点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠FDE＝∠A．
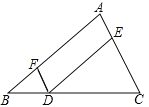
证明：∵DE∥AB，
∴∠FDE＝∠ （ ）
∵DF∥CA，
∴∠A＝∠ （ ）
∴∠FDE＝∠A（ ）
参考答案：
【答案】BFD，两直线平行，内错角相等，BFD，两直线平行，同位角相等，等量代换
【解析】
根据平行线的性质得出∠FDE=∠BFD，∠A=∠BFD，推出即可；
解：证明：∵DE∥AB，
∴∠FDE＝∠BFD（两直线平行，内错角相等）
∵DF∥CA，
∴∠A＝∠BFD（两直线平行，同位角相等）
∴∠FDE＝∠A（等量代换）．
故答案为：BFD，两直线平行，内错角相等，BFD，两直线平行，同位角相等，等量代换．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．
（1）求证：四边形DBFE是平行四边形；
（2）当△ABC满足什么条件时，四边形DBFE是菱形？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,已知
两地相距6千米,甲骑自行车从
地出发前往
地,同时乙从
地出发步行前往地.
(1)已知甲的速度为16千米/小时,乙的速度为4千米/小时,求两人出发几小时后甲追上乙；
(2)甲追上乙后,两人都提高了速度,但甲比乙每小时仍然多行12千米,甲到达
地后立即返回,两人在
两地的中点处相遇,此时离甲追上乙又经过了2小时.求
两地相距多少千米. -
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列等式：
第1个等式：
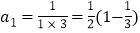
第2个等式：
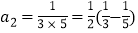
第3等式：
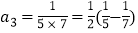
第4个等式：
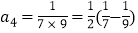
请解答下列问题：
（1）按以上规律写出第5个等式：a5= = ．
（2）用含n的式子表示第n个等式：an= = （n为正整数）．
（3）求a1+a2+a3+a4+…+a2018的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是平行四边形，E，F是对角线BD上的点，∠1=∠2.
求证：（1）BE=DF；（2）AF∥CE.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，甲、乙两车分别从相距480km的A、B两地相向而行，乙车比甲车先出发1小时，并以各自的速度匀速行驶，甲车到达C地后因有事按原路原速返回A地．乙车从B地直达A地，两车同时到达A地．甲、乙两车距各自出发地的路程y（千米）与甲车出发所用的时间x（小时）的关系如图2，结合图象信息解答下列问题：
（1）乙车的速度是 千米/时，乙车行驶的时间t= 小时；
（2）求甲车从C地按原路原速返回A地的过程中，甲车距它出发地的路程y与它出发的时间x的函数关系式；
（3）直接写出甲车出发多长时间两车相距80千米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（8分）某酒厂每天生产A，B两种品牌的白酒共600瓶，A，B两种品牌的白酒每瓶的成本和利润如下表：设每天生产A种品牌白酒x瓶，每天获利y元．
（1）请写出y关于x的函数关系式；
（2）如果该酒厂每天至少投入成本26400元，那么每天至少获利多少元？
相关试题
