搜索
【题目】某商场购进一批L型服装（数量足够多），进价为40元/件，以60元/件销售，每天销售20件，根据市场调研，若每件降价1元，则每天销售数量比原来多3件．现商场决定对L型服装开展降价促销活动，每件降价x元（x为正整数）．在促销期间，商场要想每天获得最大销售毛利润，每件应降价多少元？每天最大销售毛利润为多少？（注：每件服装销售毛利润是指每件服装的销售价与进货价的差）
参考答案：
【答案】解：设每件降价x元时，获得的销售毛利润为y元． 由题意，有y=（60﹣40﹣x）（20+3x）=﹣3x2+40x+400，
∵x为正整数，
∴当x= 
= 
≈7时，y有最大值﹣3×72+40×7+400=533．
因此，在促销期间，商场要想每天获得最大销售毛利润，每件应降价7元，此时，每天最大销售毛利润为533元
【解析】设每件降低x元时，获得的销售毛利润为y元．根据毛利润=每件服装销售毛利润×销售量列出函数关系式，再根据二次函数的性质，结合已知条件即可求出最大销售毛利润和降价元数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的口袋里装有白、红、黑三种颜色的小球，其中白球2只，红球1只，黑球1只，它们除了颜色之外没有其它区别，从袋中随机地摸出1只球，记录下颜色后放回搅匀，再摸出第二只球并记录颜色，求两次都摸出白球的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，对角线AC的中点为O，过点O作AC的垂线分别与AD、BC相交于点E、F，连接AF．求证：AE=AF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，已知△ABC和△DEF的顶点坐标分别为A（1，0）、B（3，0）、C（2，1）、D（4，3）、E（6，5）、F（4，7）．
按下列要求画图：以O为位似中心，将△ABC向y轴左侧按比例尺2：1放大得△ABC的位似图形△A1B1C1 ， 并解决下列问题：
（1）顶点A1的坐标为 ， B1的坐标为 ， C1的坐标为；
（2）请你利用旋转、平移两种变换，使△A1B1C1通过变换后得到△A2B2C2 ， 且△A2B2C2恰与△DEF拼接成一个平行四边形（非正方形），写出符合要求的变换过程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】平面上有两条直线AB、CD相交于点O，且∠BOD=150°（如图），现按如下要求规定此平面上点的“距离坐标”： ①点O的“距离坐标”为（0，0）；
②在直线CD上，且到直线AB的距离为p（p＞0）的点的“距离坐标”为（p，0）；在直线AB上，且到直线CD的距离为q（q＞0）的点的“距离坐标”为（0，q）；
③到直线AB、CD的距离分别为p，q（p＞0，q＞0）的点的“距离坐标”为（p，q）．
设M为此平面上的点，其“距离坐标”为（m，n），根据上述对点的“距离坐标”的规定，解决下列问题：
（1）画出图形（保留画图痕迹）： ①满足m=1，且n=0的点M的集合；
②满足m=n的点M的集合；
（2）若点M在过点O且与直线CD垂直的直线l上，求m与n所满足的关系式．（说明：图中OI长为一个单位长）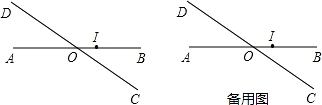
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，在矩形ABCD中，AB=4，BC=2，点M为边BC的中点，点P为边CD上的动点（点P异于C，D两点）．连接PM，过点P作PM的垂线与射线DA相交于点E（如图），设CP=x，DE=y．
（1）写出y与x之间的关系式；
（2）若点E与点A重合，则x的值为；
（3）是否存在点P，使得点D关于直线PE的对称点D′落在边AB上？若存在，求x的值；若不存在，请说明理由．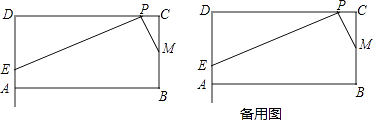
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，已知动点P在正比例函数y=x的图象上，点P的横坐标为m（m＞0），以点P为圆心，
m为半径的圆交x轴于A、B两点（点A在点B的左侧），交y轴于C、D两点（点D在点C的上方）．点E为平行四边形DOPE的顶点（如图）． 
（1）写出点B、E的坐标（用含m的代数式表示）；
（2）连接DB、BE，设△BDE的外接圆交y轴于点Q（点Q异于点D），连接EQ、BQ，试问线段BQ与线段EQ的长是否相等？为什么？
（3）连接BC，求∠DBC﹣∠DBE的度数．
相关试题
