【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.

(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
参考答案:
【答案】30°;见解析.
【解析】
试题分析:根据∠ACB和∠B的度数得出∠CAB的度数,根据角平分线的性质得出∠CAD的度数;根据∠ACD+∠ECD=180°,∠ACD=90°得出∠ACD=∠ECD=90°,证明△ACD和△ECD全等,从而得出结论.
试题解析:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°, ∴∠CAB=60°.
又∵AD平分∠CAB, ∴∠CAD=![]() ∠CAB=30°,即∠CAD=30°;
∠CAB=30°,即∠CAD=30°;
(2)证明:∵∠ACD+∠ECD=180°,且∠ACD=90°, ∴∠ECD=90°, ∴∠ACD=∠ECD.
在△ACD与△ECD中,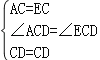 , ∴△ACD≌△ECD(SAS), ∴DA=DE.
, ∴△ACD≌△ECD(SAS), ∴DA=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)
=
(2)
+ =
= 
(3)先化简,再求值( ﹣
﹣  )÷
)÷  ,其中a=1,b=2.
,其中a=1,b=2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°,若抛物线 y=x+k与扇形OAB的边界总有两个公共点,则实数取值范围是

A. -4<k<
 B. -2<k<
B. -2<k<
C. -4<k<
 D. --2<k<
D. --2<k<
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A(体操)、B(乒乓球)、C(毽球)、D(跳绳)四项活动.为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:

(1)这次被调查的学生共有人;
(2)请将统计图2补充完整;
(3)统计图1中B项目对应的扇形的圆心角是度;
(4)已知该校共有学生1000人,根据调查结果估计该校喜欢体操的学生有人. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
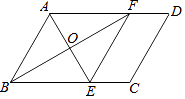
(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE= ,求ABCD的面积.
,求ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:4+x=3x﹣2.
相关试题

