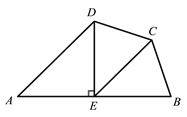
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边的垂直平分线,连接
边的垂直平分线,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)由线段垂直平分线的性质得到AE=EB=4,再由∠A=45°,得到DE=AE=EB,由“SSS”公理即可得到△EDC≌△EBC,由全等三角形对应角相等即可得出结论;
(2)过点C作CH⊥AB于点H,即可得到CH=EH.设EH=x,则BH=4-x.在Rt△CHB中,由勾股定理可求出x的值,由CE=![]() EH即可得到结论.
EH即可得到结论.
详解:(1)∵![]() 是
是![]() 边的垂直平分线,
边的垂直平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴△![]() ≌△
≌△![]() .
.

∴![]() .
.
(2)过点![]() 作
作![]() 于点
于点![]() ,可得:
,可得:![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得:![]() (不合题意,舍去),
(不合题意,舍去),
即![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(﹣4,4),一个以A为顶点的45°角绕点A旋转,角的两边分别交x轴正半轴,y轴负半轴于E、F,连接EF.当△AEF是直角三角形时,点E的坐标是_____

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学进行长跑训练,甲和乙所跑的路程S(单位:米)与所用时间t(单位:秒)之间的函数图象分别为线段OA和折线OBCD.则下列说法正确的是( )
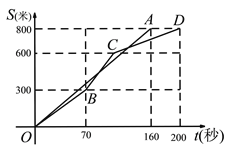
A. 两人从起跑线同时出发,同时到达终点
B. 跑步过程中,两人相遇一次
C. 起跑后160秒时,甲、乙两人相距最远
D. 乙在跑前300米时,速度最慢
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在四边形ABCD中,∠ABC=∠ADC=90,M、N分别是CD和BC上的点.
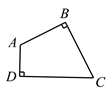
求作:点M、N,使△AMN的周长最小.
作法:如图,
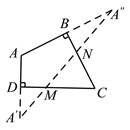
(1)延长AD,在AD的延长线上截取DA=DA;
(2)延长AB,在AB的延长线上截取B A″=BA;
(3)连接A′A″,分别交CD、BC于点M、N.则点M、N即为所求作的点.
请回答:这种作法的依据是_____________.
-
科目: 来源: 题型:
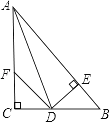
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
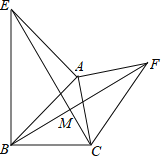
求证:(1)EC=BF;
(2)EC⊥BF;
(3)连接AM,求证:AM平分∠EMF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,直线
中,直线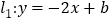 与
与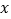 轴,
轴,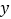 轴分别交于点
轴分别交于点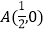 ,B,与反比例函数图象的一个交点为
,B,与反比例函数图象的一个交点为 .
.(1)求反比例函数的表达式;
(2)设直线
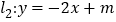 与
与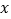
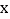 轴,
轴,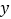 轴分别交于点C,D,且
轴分别交于点C,D,且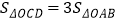 ,直接写出
,直接写出 的值 .
的值 .
相关试题

