【题目】如图,已知点A(﹣4,4),一个以A为顶点的45°角绕点A旋转,角的两边分别交x轴正半轴,y轴负半轴于E、F,连接EF.当△AEF是直角三角形时,点E的坐标是_____

参考答案:
【答案】(8,0)或(4,0)
【解析】
当∠AFE=90°,可证明△ADF≌△FOE,则FO=AD=4,OE=DF=OD+FC=8,从而可求得点E坐标,同理当∠AEF=90°时,也可求得点E坐标.
解:①如图所示:当∠AFE=90°,
∴∠AFD+∠OFE=90°,
∵∠OEF+∠OFE=90°,
∴∠AFD=∠OEF
∵∠AFE=90°,∠EAF=45°,
∴∠AEF=45°=∠EAF,
∴AF=EF,
在△ADF和△FOE中,
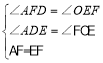
∴△ADF≌△FOE(AAS),
∴FO=AD=4,OE=DF=OD+FO=8,
∴E(8,0)
②当∠AEF=90°时,同①的方法得,OF=8,OE=4,
∴E(4,0),
综上所述,满足条件的点E坐标为(8,0)或(4,0)

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(
 ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, 分别为
分别为 ,
, 边上的高,连接
边上的高,连接 ,过点
,过点 作
作 与点
与点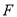 ,
, 为
为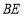 中点,连接
中点,连接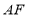 ,
, .
.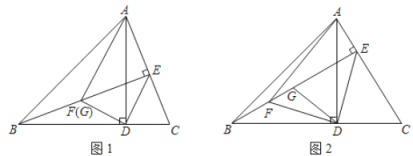
(1)如图
 ,若点
,若点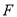 与点
与点 重合,求证:
重合,求证: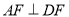 ;
;(2)如图
 ,请写出
,请写出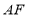 与
与 之间的关系并证明.
之间的关系并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于
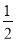 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若AC=9,AB=15,且S△ABC=54,则△ABD的面积是( )
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若AC=9,AB=15,且S△ABC=54,则△ABD的面积是( )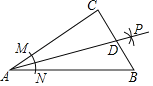
A.
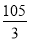 B.
B. 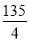 C. 45D. 35
C. 45D. 35 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学进行长跑训练,甲和乙所跑的路程S(单位:米)与所用时间t(单位:秒)之间的函数图象分别为线段OA和折线OBCD.则下列说法正确的是( )
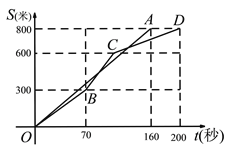
A. 两人从起跑线同时出发,同时到达终点
B. 跑步过程中,两人相遇一次
C. 起跑后160秒时,甲、乙两人相距最远
D. 乙在跑前300米时,速度最慢
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在四边形ABCD中,∠ABC=∠ADC=90,M、N分别是CD和BC上的点.
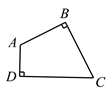
求作:点M、N,使△AMN的周长最小.
作法:如图,
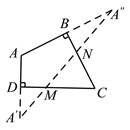
(1)延长AD,在AD的延长线上截取DA=DA;
(2)延长AB,在AB的延长线上截取B A″=BA;
(3)连接A′A″,分别交CD、BC于点M、N.则点M、N即为所求作的点.
请回答:这种作法的依据是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
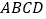 中,
中,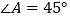 ,
,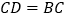 ,
,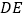 是
是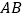 边的垂直平分线,连接
边的垂直平分线,连接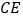 .
.(1)求证:
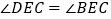 ;
;(2)若
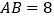 ,
, ,求
,求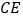 的长.
的长.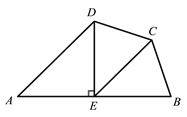
相关试题

