【题目】矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为多少?

参考答案:
【答案】![]()
【解析】试题分析:根据矩形的性质,可得AB与CD的关系,根据翻折的性质,可得∠FEA=∠FEC;AD与CG的关系,根据全等三角形的判定与性质,可得FG与BE的关系,根据勾股定理,可得BE的长,根据面积的和差,可得答案.
试题解析:∵ABCD是矩形, ∴AB||CD,
∴∠FEA=∠EFC,
∵将矩形纸片沿EF折叠,使点A与点C重合,∴∠FEA=∠FEC,
∴∠EFC=∠FEC,
∴CF=CE,
∵将矩形纸片沿EF折叠,使点A与点C重合,∴CG=AD=2,
∵ABCD是矩形,∴AD=BC,
∴CG=BC,
在Rt△CGF和Rt△CBE中, ![]() ,∴△CGF≌△CBE(HL),∴FG=BE,
,∴△CGF≌△CBE(HL),∴FG=BE,
设AE=CE=x,则BE=FG=(4﹣x),
在Rt△BCE中,EC2=EB2+BC2 ,即(4﹣x)2+22=x2,
x=![]() ,BE=
,BE=![]() ,
,
∵CF=AE= ![]() ,∴DF=BE=
,∴DF=BE=![]() ,
,
∴S着色=S四边形BEFC+S△CFG=![]() (BE+CF)BC+
(BE+CF)BC+![]() CGFG=
CGFG= ![]() ×(
×( ![]() +
+ ![]() )×2+
)×2+ ![]() ×2×
×2×![]() =4+
=4+ ![]() =
= ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y= ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x
...
-3
-2
- 1
0
1
...
y
...
-6
0
4
6
6
...
容易看出,(-2,0)是抛物线与x轴的一个交点,则它与x轴的另一个交点的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)
根据实验,小雨很快就把四个编好号的大西瓜的质量由小到大排列起来了.你认为小雨的实验于结果都是真实的吗?(即通过上述实验能找出它们质量的大小吗?)请说明你的理由,并与同学交流.

-
科目: 来源: 题型:
查看答案和解析>>【题目】关于
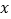 的方程
的方程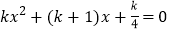 有实数根.
有实数根.(1)求
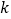 的取值范围;
的取值范围;(2)是否存在实数
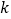 ,使方程的两个实数根的倒数和等于0 ?若存在,求出
,使方程的两个实数根的倒数和等于0 ?若存在,求出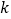 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在(ax+3y)与(x﹣y)的积中,不含有xy项,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 。
。(1)求顶点坐标,对称轴;
(2)
 取何值时,
取何值时,  随
随 的增大而减小?
的增大而减小?(3)
 取何值时,
取何值时,  =0;
=0;  取何值时,
取何值时,  >0;
>0;  取何值时,
取何值时,  <0 。
<0 。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在同一平面直角坐标系中,正比例函数
 与二次函数y=-x2+2x+c的图象交于点A(-1,m).
与二次函数y=-x2+2x+c的图象交于点A(-1,m).(1)求m,c的值;
(2)求二次函数图象的对称轴和顶点坐标.
相关试题

