【题目】关于![]() 的方程
的方程![]() 有实数根.
有实数根.
(1)求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使方程的两个实数根的倒数和等于0 ?若存在,求出
,使方程的两个实数根的倒数和等于0 ?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ≥
≥![]() (2)
(2)![]() 不存在.
不存在.
【解析】(1)利用方程有两根不相等的实数根可以得到△=(m+2)2-4m![]() >0,解得m的取值范围即可;
>0,解得m的取值范围即可;
(2)假设存在,然后利用根的判别式求得m的值,根据m的值是否能使得一元二次方程有实数根作出判断即可.
解:(1)当![]() =0时,方程是一元一次方程,此时方程的根为x=0.方程有根
=0时,方程是一元一次方程,此时方程的根为x=0.方程有根
当![]() ≠0时,方程为一元二次方程,△=
≠0时,方程为一元二次方程,△=![]() ≥0,得:
≥0,得:![]() ≥
≥![]() 且
且![]() ≠0).
≠0).
综上所述k的取值范围是![]() ≥
≥![]()
(2)不存.在假设存在满足条件的实数![]() ,方程的两个根是
,方程的两个根是![]() 、
、![]() ,
,
∵![]() =
=![]() ≠0,∴
≠0,∴![]() =
=![]() =0,∴
=0,∴![]() +
+![]() =0,
=0,
∵![]() +
+![]() =
=![]() ,∴
,∴![]() ,即
,即![]()
![]() ,
,
∴满足条件的实数![]() 不存在.
不存在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿射线AB,BC运动,且它们的速度都为2cm/s.设点P的运动时间为t(s).
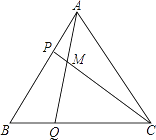
(1)当t为何值时,△ABQ≌△CBP.
(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y= ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x
...
-3
-2
- 1
0
1
...
y
...
-6
0
4
6
6
...
容易看出,(-2,0)是抛物线与x轴的一个交点,则它与x轴的另一个交点的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)
根据实验,小雨很快就把四个编好号的大西瓜的质量由小到大排列起来了.你认为小雨的实验于结果都是真实的吗?(即通过上述实验能找出它们质量的大小吗?)请说明你的理由,并与同学交流.

-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在(ax+3y)与(x﹣y)的积中,不含有xy项,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 。
。(1)求顶点坐标,对称轴;
(2)
 取何值时,
取何值时,  随
随 的增大而减小?
的增大而减小?(3)
 取何值时,
取何值时,  =0;
=0;  取何值时,
取何值时,  >0;
>0;  取何值时,
取何值时,  <0 。
<0 。
相关试题

