【题目】如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,﹣2),点D的横坐标为![]() , 将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
, 将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
(1)图中,∠OCE等于多少;
(2)求抛物线的解析式;
(3)抛物线上是否存在点P,使S△PAE=![]() S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.
S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】解:(1)∵△CDE绕点C旋转到△CBO,
∴∠OCE=∠BCD;
故答案为BCD;
(2)作CH⊥OE于H,如图,
∵△CDE绕点C旋转到△CBO,
∴CO=CE,CB=CD,OB=DE,
∴OH=HE=1,
∴OE=2,
∴E点坐标为(2,0),
设B(m,0),D(![]() ,n),
,n),
∵CD2=(1﹣![]() )2+(﹣2﹣n)2 , CB2=(1﹣m)2+22 , DE2=(2﹣
)2+(﹣2﹣n)2 , CB2=(1﹣m)2+22 , DE2=(2﹣![]() )2+n2 ,
)2+n2 ,
∴(1﹣![]() )2+(﹣2﹣n)2=(1﹣m)2+22 , (2﹣
)2+(﹣2﹣n)2=(1﹣m)2+22 , (2﹣![]() )2+n2=m2 ,
)2+n2=m2 ,
∴m=3,n=﹣![]() ,
,
∴B(3,0),
设抛物线解析式为y=a(x﹣1)2﹣2,
把B(3,0)代入得4a﹣2=0,解得a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣1)2﹣2,即y=
(x﹣1)2﹣2,即y=![]() x2﹣x﹣
x2﹣x﹣![]() ;
;
(3)存在.
A与点B关于直线x=1对称,
∴A(﹣1,0),
∵△CDE绕点C旋转到△CBO,
∴△CDE≌△CBO,
∴S△CDE=S△CBO=![]() 23=3,
23=3,
设P(t,![]() t2﹣t﹣
t2﹣t﹣![]() ),
),
∵S△PAE=![]() S△CDE ,
S△CDE ,
∴![]() 3|
3|![]() t2﹣t﹣
t2﹣t﹣![]() |=
|=![]() 3,
3,
∴![]() t2﹣t﹣
t2﹣t﹣![]() =1或
=1或![]() t2﹣t﹣img src="http://thumb.zyjl.cn/questionBank/Upload/2017/02/11/01/c4094a12/SYS201702110154341163223416_DA/SYS201702110154341163223416_DA.005.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />=﹣1,
t2﹣t﹣img src="http://thumb.zyjl.cn/questionBank/Upload/2017/02/11/01/c4094a12/SYS201702110154341163223416_DA/SYS201702110154341163223416_DA.005.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />=﹣1,
解方程![]() t2﹣t﹣
t2﹣t﹣![]() =1得t1=1+
=1得t1=1+![]() ,t2=1﹣
,t2=1﹣![]() ,此时P点坐标为(1+
,此时P点坐标为(1+![]() ,1)或(1﹣
,1)或(1﹣![]() ,1);
,1);
解方程![]() t2﹣t﹣
t2﹣t﹣![]() =﹣1得t1=1+
=﹣1得t1=1+![]() ,t2=1﹣
,t2=1﹣![]() ,此时P点坐标为(1+
,此时P点坐标为(1+![]() ,﹣1)或(1﹣
,﹣1)或(1﹣![]() ,1);
,1);
综上所述,满足条件的P点坐标为(1+![]() ,1)或(1﹣
,1)或(1﹣![]() ,1)或(1+
,1)或(1+![]() ,﹣1)或(1﹣
,﹣1)或(1﹣![]() ,1).
,1).
【解析】(1)根据旋转的性质易得∠OCE=∠BCD;
(2)作CH⊥OE于H,如图,根据旋转的性质得CO=CE,CB=CD,OB=DE,则利用等腰三角形的性质得OH=HE=1,则E点坐标为(2,0),设B(m,0),D(![]() , n),利用两点间的距离公式得CD2=(1﹣
, n),利用两点间的距离公式得CD2=(1﹣![]() )2+(﹣2﹣n)2 , CB2=(1﹣m)2+22 , DE2=(2﹣
)2+(﹣2﹣n)2 , CB2=(1﹣m)2+22 , DE2=(2﹣![]() )2+n2 , 所以(1﹣
)2+n2 , 所以(1﹣![]() )2+(﹣2﹣n)2=(1﹣m)2+22 , (2﹣
)2+(﹣2﹣n)2=(1﹣m)2+22 , (2﹣![]() )2+n2=m2 , 解关于m、n的方程组得到m=3,n=﹣
)2+n2=m2 , 解关于m、n的方程组得到m=3,n=﹣![]() , 则B(3,0),然后设顶点式y=a(x﹣1)2﹣2,再把B点坐标代入求出a即可得到抛物线解析式;
, 则B(3,0),然后设顶点式y=a(x﹣1)2﹣2,再把B点坐标代入求出a即可得到抛物线解析式;
(3)先利用抛物线的对称性得到A(﹣1,0),再根据旋转的性质得△CDE≌△CBO,则S△CDE=S△CBO=3,设P(t,![]() t2﹣t﹣
t2﹣t﹣![]() ),利用三角形面积公式得到
),利用三角形面积公式得到![]() 3|
3|![]() t2﹣t﹣
t2﹣t﹣![]() |=
|=![]() 3,则
3,则![]() t2﹣t﹣
t2﹣t﹣![]() =1或
=1或![]() t2﹣t﹣
t2﹣t﹣![]() =﹣1,然后分别解关于t的一元二次方程求出t,从而可得到满足条件的P点坐标.
=﹣1,然后分别解关于t的一元二次方程求出t,从而可得到满足条件的P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D是AB边上一点(不与AB重合),AD=kBD,过点D作∠EDF+∠C=180°,与CA、CB分别交于E、F.
(1)如图1,当DE=DF时,求 的值.
的值.
(2)如图2,若∠ACB=90°,∠B=30°,DE=m,求DF的长(用含k,m的式子表示)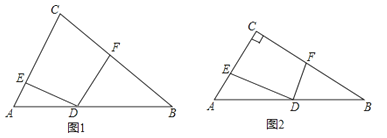
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,P是BC中点,∠EPF=90°,给出四个结论:①∠B=∠BAP;②AE=CF;③PE=PF;④S四边形AEPF=
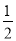 S△ABC.其中成立的有_______
S△ABC.其中成立的有_______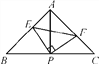
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙P的半径为2,圆心P在抛物线y=
 x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为
x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为 
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
相关试题

