【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
(1)设△POQ的面积为s,写出s关于t的函数关系式;当t为何值时,△POQ的面积最大,这时面积是多少
(2)当t为何值时,△POQ与△AOB相似?

参考答案:
【答案】(1) s=-![]() t2+3t; 当t=3时,s有最大值
t2+3t; 当t=3时,s有最大值![]() .(2)t=4或t=2
.(2)t=4或t=2
【解析】
试题分析:(1)根据P、Q的速度,用时间t表示出OQ和OP的长,即可通过三角形的面积公式得出s,t的函数关系式;根据函数式求出s最大时即可;
(3)本题要分△OPQ∽△OAB和△OPQ∽△OBA两种情况进行求解,可根据各自得出的对应成比例相等求出t的值.
试题解析:(1)由题意可知,s=![]() (6-t)t=-
(6-t)t=-![]() t2+3t, (0≤t≤6)
t2+3t, (0≤t≤6)
配方得,s=-![]() t2+3t=-
t2+3t=-![]() (t-3)2+
(t-3)2+![]() ,
,
因为-![]() <0,所以,当t=3时,s有最大值
<0,所以,当t=3时,s有最大值![]() .
.
(2)①若△POQ∽△AOB时,![]() ,即
,即![]() ,
,
整理得:12-2t=t,
解得:t=4.
②若△POQ∽△BOA时,![]() ,即
,即![]() ,
,
整理得:6-t=2t,解得:t=2.
∵0≤t≤6,
∴t=4和t=2均符合题意,
∴当t=4或t=2时,△POQ与△AOB相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
2,﹣4,8,﹣16,32,﹣64,…; ①
4,﹣2,10,﹣14,34,﹣62,…;②
1,﹣2,4,﹣8,16,﹣32,….③
(1)第①行第8个数为;第②行第8个数为;第③行第8个数为;
(2)第③行中是否存在连续的三个数,使得三个数的和为768?若存在,则求出这三数;不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=kx(k≠0)的图象过P(﹣3,3),则k=________,图象过________象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式
 =1﹣
=1﹣  ,
, 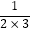 =
=  ﹣
﹣  ,
, 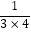 =
=  ﹣
﹣  ,把以上三个等式两边分别相加得:
,把以上三个等式两边分别相加得:  +
+ 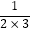 +
+ 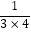 =1﹣
=1﹣  +
+  ﹣
﹣  +
+  ﹣
﹣  =1﹣
=1﹣  =
=  .
.
(1)猜想并写出: = .
= .
(2)直接写出下列各式的计算结果:
① +
+ 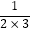 +
+ 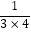 +…+
+…+ 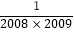 =;
=;
② +
+ 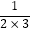 +
+ 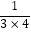 +…+
+…+  = .
= .
(3)探究并计|算: +…+
+…+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).

(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中,放入分别标注1、﹣2、3三个不同数字的小球,小球除了数字不同外,其余都相同.小明闭上眼睛先把小球搅均,再从该布袋中摸出第一个小球,记小球上的数字为A,把球重新放回布袋中搅均,摸出第二个小球,记小球上的数字为B.
(1)求小明第一次摸出的小球上的数字为“负数”的概率;
(2)求两次摸出的小球上的数字均是一元一次不等式2x+3>0的解的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,若∠C=90°,cosA=
 ,则sinA的值为()
,则sinA的值为()
A.
B.
C.
D.
相关试题

