搜索
【题目】已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．
（1）画出△ABC向下平移4个单位长度得到的△A1B1C1 ， 点C1的坐标是；
（2）以点B为位似中心，在网格内画出△A2B2C2 ， 使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是；
（3）△A2B2C2的面积是平方单位．
参考答案：
【答案】
（1）（2，﹣2）
（2）（1，0）
（3）10
【解析】解：（1）如图所示：C1（2，﹣2）；
故答案为：（2，﹣2）；（2）如图所示：C2（1，0）；
故答案为：（1，0）；（3）∵A2C22=20，B2C 
=20，A2B2 
=40，
∴△A2B2C2是等腰直角三角形，
∴△A2B2C2的面积是： 
×20=10平方单位．
故答案为：10．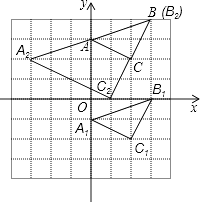
（1）利用平移的性质得出平移后图象进而得出答案；（2）利用位似图形的性质得出对应点位置即可；（3）利用等腰直角三角形的性质得出△A2B2C2的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知y是关于x的一次函数，且当x=1时，y=﹣4；当x=2时，y=﹣6.
(1)求y关于x的函数表达式；
(2)若﹣2＜x＜4，求y的取值范围；
(3)试判断点P(a，﹣2a+3)是否在函数的图象上，并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在5×4的网格中，每个小正方形的边长是1个单位长.
（1）先在图中将面积是5的一个长方形分割成5块，然后再画出用这5块拼成的一个正方形；
（2）设拼成的正方形的边长为a个单位长，
①a是有理数还是无理数？
②试在数轴上将a的相反数表示出来；
③求出a的近似值（保留一位小数）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．
（1）求证：四边形AECF是菱形；
（2）若AB=
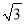，∠DCF=30°，求四边形AECF的面积．（结果保留根号）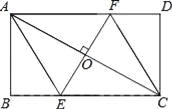
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图
，
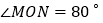，点A、B在
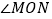的两条边上运动，
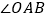与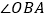
的平分线交于点C．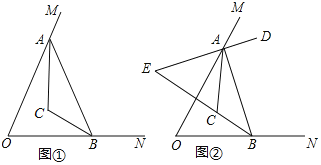
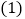点A、B在运动过程中，
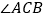的大小会变吗？如果不会，求出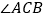的度数；如果会，请说明理由．
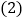如图
，AD是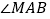
的平分线，AD的反向延长线交BC的延长线于点E，点A、B在运动过程中，
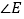的大小会变吗？如果不会，求出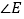的度数；如果会，请说明理由．
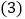若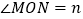
，请直接写出
______；
______． -
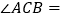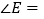科目： 来源： 题型：
查看答案和解析>>【题目】a、b、c在数轴上的位置如图所示，则：
（1）用“＜、＞、＝”填空：a____0，b____0，c_____0；
（2）用“＜、＞、＝”填空：﹣a____0，a﹣b____0，c﹣a____0；
（3）化简：|﹣a|﹣|a﹣b|+|c﹣a|
-
科目： 来源： 题型：
查看答案和解析>>【题目】将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0)，MN平行于y轴，E是BC的中点，现将纸片折叠，使点C落在MN上，折痕为直线EF.
(1)求点G的坐标；
(2)求直线EF的解析式；
(3)设点P为直线EF上一点，是否存在这样的点P，使以P, F, G的三角形是等腰三角形?若存在，直接写出P点的坐标;若不存在，请说明理由.
相关试题
