【题目】在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.
(1)如图1,试判断四边形EGFH的形状,并说明理由; 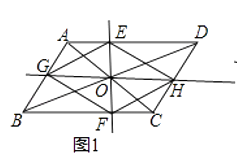
(2)如图2,当EF⊥GH,AC=BD时,四边形EGFH的形状是; 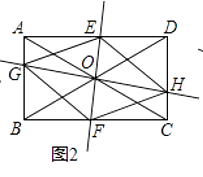
(3)在(2)的条件下,若AC⊥BD(如图3),四边形EGFH的形状是 . 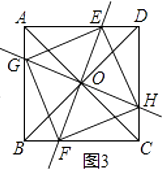
参考答案:
【答案】
(1)解:四边形EGFH是平行四边形.
证明:∵平行四边形ABCD的对角线AC、BD交于点O.
∴点O是ABCD的对称中心.
∴EO=FO,GO=HO.
∴四边形EGFH是平行四边形
(2)菱形
(3)正方形
【解析】解:(2)∵四边形EGFH是平行四边形,EF⊥GH,AC=BD
∴四边形EGFH是菱形;
所以答案是:菱形;
⑶四边形EGFH是正方形;理由如下
∵AC=BD,
∴ABCD是矩形;
又∵AC⊥BD,
∴ABCD是正方形,
∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;
∵EF⊥GH,
∴∠GOF=90°;
∠BOG+∠BOF=∠COF+∠BOF=90°
∴∠BOG=∠COF;
∴△BOG≌△COF(ASA);
∴OG=OF,同理可得:EO=OH,
∴GH=EF;
由(2)知四边形EGFH是菱形,
又EF=GH,
∴四边形EGFH是正方形.
所以答案是:正方形.
【考点精析】通过灵活运用平行四边形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为 .
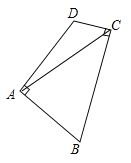
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明根据华师版八年级下册教材P37学习内容,对函数y=
 x2的图象和性质进行了探究,试将如下尚不完整的过程补充完整.
x2的图象和性质进行了探究,试将如下尚不完整的过程补充完整. 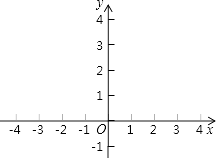
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:x
…
﹣4
n
﹣2
﹣1
0
1
2
3
4
…
y
…
8
4.5
2
0.5
0
0.5
2
4.5
8
…
其中n=;
(2)如图,在平面直角三角形坐标系xOy中,已描出了以上表中的部分数值为坐标的点,根据描出的点,画出该函数的大致图象.
(3)根据画出的函数图象,小明观察发现:该函数有最小值,没有最大值;当函数值取最小时,自变量x的值为 .
(4)进一步探究函数的图象发现: ①若点A(xa , ya),点B(xb , yb)在函数y=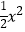 的图象上;
的图象上;
当xa<xb<0时,ya与yb的大小关系是;
当0<xa<xb时,ya与yb的大小关系是;
②直线y1恰好经过函数的图象上的点(﹣2,2)与(1,0.5);当y<y1时,x的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】长为8,5,4,3的四根木条,选其中三根组成三角形,选法有( )
A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-2)2018+(-2)2019等于( )
A. -24037 B. -2 C. -22018 D. 22018
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师测量跳远成绩的依据是( )
A. 两点确定一条直线B. 两点之间,线段最短
C. 垂线段最短D. 平行线间的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形有一个内角是120°,那么这个正多边形是正_____边形.
相关试题

