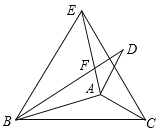
【题目】如图,将△ABC 分别沿 AB,AC 翻折得到△ABD 和△AEC,线段 BD 与AE 交于点 F.
(1)若∠ABC=16,∠ACB=30°,求∠DAE 及∠BFE 的值;
(2)若 BD 与 CE 所在的直线互相垂直,求∠CAB 的度数.
参考答案:
【答案】(1)42°,108°;(2)135°.
【解析】
由“∠ABC=16,∠ACB=30°”可以求出∠BAC的度数,根据翻折的性质可以求出∠DAE与∠BFE的度数,由“BD 与 CE 所在的直线互相垂直”可得∠DBC+∠ECB=90°,再利用翻折的性质可求出答案
解:(1)∵∠ABC=16°,∠ACB=30°,
∴∠BAC=134°,
∵△ABC≌△ABD,△ABC≌△AEC,
∴∠BAD=∠EAC=134°;∠DAE=134°×3-360°=42°.
∵∠D=∠ACB=30°,
∴∠BFE=∠DFA=180°-42°-30°=108°;
(2)∵BD 所在直线与 CE 所在直线互相垂直,
∴∠DBC+∠ECB=90°,
∵翻折
∴∠ABC=![]() ∠DBC ∠ACB =
∠DBC ∠ACB =![]() ∠ECB
∠ECB
∴∠ABC+∠ACB= ![]() ( ∠DBC+∠ECB )=45°,
( ∠DBC+∠ECB )=45°,
∴∠CAB=180°-(∠ABC+∠ACB )= 135°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新型冠状病毒爆发,教育部部署了“停课不停学”的有关工作,各地都在进行在线教育.小依同学为了了解网课学习情况,对本班部分同学最喜爱的课程进行了调查,调查课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程并制成以下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
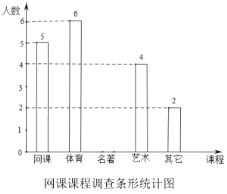
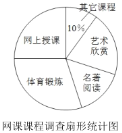
(1)本次调查中一共调查了__________名学生,其中“名著阅读”所占的圆心角度数为__________.
(2)请把条形统计图补全.
(3)在调查的同学中随机选取一名学生,求他恰好最喜爱的课程是“艺术欣赏”的概率.
(4)若该校一共有3000名学生,请估算出全校最喜爱的课程是“体育锻炼”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点
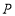 从点
从点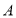 出发沿图1的边框(边框拐角处都互相垂直)按
出发沿图1的边框(边框拐角处都互相垂直)按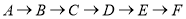 的路径移动,相应的
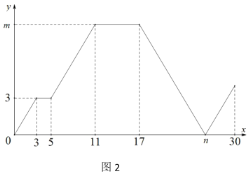
的路径移动,相应的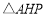 的面积
的面积 关于移动路程
关于移动路程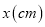 的关系图象如图2,若
的关系图象如图2,若 ,根据图象信息回答下列问题:
,根据图象信息回答下列问题:(1)图1中
 ___________
___________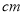 .
.(2)图2中
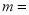 ___________;
___________;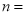 ___________.
___________.(3)当
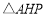 的面积
的面积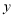 为2时,求对应的
为2时,求对应的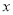 的值.
的值.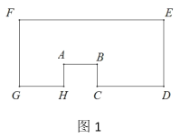
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BF 是∠ABD 的平分线,CE 是∠ACD 的平分线,BF 与 CE 交于 G,若∠BDC=130°,∠BGC=100°,则∠A 的度数为( )
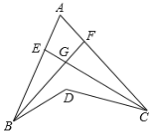
A.60°B.70°C.80°D.90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明和小龙做转陀螺游戏,他们同时分别转动一个陀螺,当两个陀螺都停下来时,与桌面相接触的边上的数字都是奇数的概率是
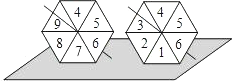
-
科目: 来源: 题型:
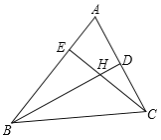
查看答案和解析>>【题目】如图,在△ABC 中,记∠A=x 度,回答下列问题:
(1)图中共有三角形 个.
(2)若 BD,CE 为△ABC 的角平分线,则∠BHC= 度(结果用含 x 的代数式
表示),并证明你的结论.
(3)若 BD,CE 为△ABC 的高线,则∠BHC= 度(结果用含 x 的代数式表示),并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
数学中枚举法是一种重要归纳法也称为列举法、穷举法,是暴力策略的具体体现,又称为蛮力法.用枚举法解题时应该注意:
1、常常需要将对象进行恰当分类.
2、使其确定范围尽可能最小,逐个试验寻求答案.
正整数
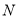 的末尾为5称为“威武数”,那么
的末尾为5称为“威武数”,那么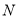 的平方数为
的平方数为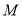 称为“平武数”.
称为“平武数”.例:
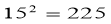
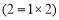 ,
,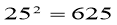
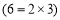 ,
,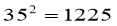
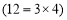 ,
,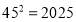
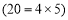 ,
,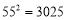
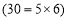 ,
,……
由以上的枚举可以归纳得到的“平武数”特点是:
①“平武数”的末两位数字是25;
②去掉末两位数字25后,剩下部分组成的数字等于“平武数”去掉个位数字5后剩部分组成的数字与比此数大1的数之积.(如例中的括号内容)
(1)根据以上特点我们能够很快的推出一个四位数的“平武数”
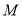 一共有___________个.
一共有___________个.(2)同学们用学过的完全平方公式求证:当“威武数”
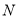 为任意二位数时“平武数”
为任意二位数时“平武数”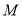 都满足以上特点.
都满足以上特点.(3)已知“平武数”
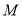 的首位数是2且小于六位,又满足
的首位数是2且小于六位,又满足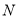 的各位数字之和与
的各位数字之和与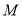 的各位数字之和相等,求出“平武数”
的各位数字之和相等,求出“平武数”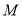 的值.
的值.
相关试题

