【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
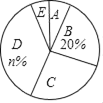
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)郑州市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?
参考答案:
【答案】(1)150,45,36;(2)28.8°;(3)散步,6%;(4)450.
【解析】
(1)由![]() 项目的人数及其百分比求得总人数,根据各项目人数之和等于总人数求得
项目的人数及其百分比求得总人数,根据各项目人数之和等于总人数求得![]() ,再用
,再用![]() 项目人数除以总人数可得
项目人数除以总人数可得![]() 的值;
的值;
(2)![]() 乘以
乘以![]() 项目人数占总人数的比例可得;
项目人数占总人数的比例可得;
(3)由表可知样本中散步人数最多,据此可得,再用![]() 项目人数除以总人数可得;
项目人数除以总人数可得;
(4)总人数乘以样本中![]() 人数所占比例.
人数所占比例.
解:(1)接受问卷调查的共有![]() 人,
人,![]() ,
,
![]() ,
,
![]() ,
,
故答案为:150、45、36;
(2)![]() 类所对应的扇形圆心角的度数为
类所对应的扇形圆心角的度数为![]() ,
,
故答案为:![]() ;
;
(3)根据调查结果,我市市民最喜爱的运动方式是散步,不运动的市民所占的百分比是![]() ,
,
故答案为:散步、![]() ;
;
(4)![]() (人
(人![]() ,
,
答:估计该社区参加碧沙岗“暴走团”的大约有450人.
-
科目: 来源: 题型:
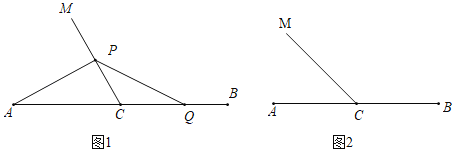
查看答案和解析>>【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(
 ,
, )
)B. 当m>0时,函数图象截x轴所得的线段长度大于

C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>
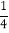 时,y随x的增大而减小
时,y随x的增大而减小 -
科目: 来源: 题型:
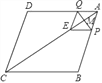
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是斜边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:BD=AF;
(2)判断四边形ADCF的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
相关试题

