【题目】如图,在△ABC中,∠BAC=90°,AD是斜边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:BD=AF;
(2)判断四边形ADCF的形状,并证明你的结论.

参考答案:
【答案】(1)见解析;(2) 四边形ADCF是菱形,理由见解析.
【解析】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,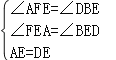 ,
,
∴△AFE≌△DBE(AAS),
∴BD=AF;
(2)解:四边形ADCF是菱形;理由如下:
由(1)知,AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=![]() BC,
BC,
∴四边形ADCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察一列数a1=3,a2=32,a3=33,a4=34,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a6=_______,an=_______;(可用幂的形式表示)
(2)如果想要求l+2+22+23+...+210的值,可令S10=l+2+22+23+...+210①,将①式两边同乘以2,得_______②,由②减去①式,得S10=_______.
(3)若(1)中数列共有20项,设S20=3+32+33+34+…+320,请利用上述规律和方法计算S20的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5,BC=12,CD=
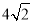 ,∠C=45°,点P是BC边上一动点,设PB的长为x。
,∠C=45°,点P是BC边上一动点,设PB的长为x。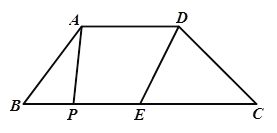
(1)梯形ABCD的面积为_________;
(2)当x的值为___________时,以点P、A、D、E为顶点的四边形为直角梯形;
(3)当x的值为___________时,以点P、A、D、E为顶点的四边形为平行四边形;
(4)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行射击测试,每人20次射击成绩的平均数都是8.5环,方差分别是:S甲2=3,S乙2=2.5,则射击成绩较稳定的是(填“甲”或“乙”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】会同县2017年1月份某天的最高气温是6℃,最低气温是-1℃,这一天会同的温差是( )
A. -7℃ B. 5℃ C. 6℃ D. 7℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明要测量公园北湖水隔开的两棵大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°方向.
(1)求∠ABC的度数;
(2)求两棵大树A和B之间的距离(结果精确到1米)(参考数据:
 ≈1.414,
≈1.414,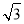 ≈1.732,
≈1.732,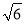 ≈2.449)
≈2.449)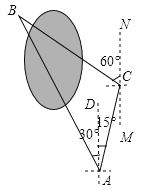
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+mx+n可以由抛物线y=x2向下平移2个单位,再向右平移3个单位得到,则mn值为 .
相关试题

