【题目】据图回答下列问题![]()
(1)数轴上表示5与﹣2两点之间的距离是 ,
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)如果|x﹣2|=5,则x= .
(4)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
(5)由以上探索猜想对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
参考答案:
【答案】
(1)7
(2),x﹣2,
(3)7或﹣3
(4)﹣3、﹣2、﹣1、0、1
(5)解:有最小值是3
【解析】解:(1)数轴上表示5与﹣2两点之间的距离是|5﹣(﹣2)|=|5+2|=7,所以答案是:7;
(2)数轴上表示x与2的两点之间的距离可以表示为|x﹣2|,所以答案是:|x﹣2|;(3)∵|x﹣2|=5,
∴x﹣2=5或x﹣2=﹣5,
解得:x=7或x=﹣3,
所以答案是:7或﹣3;(4)∵|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,|x+3|+|x﹣1|=4,
∴这样的整数有﹣3、﹣2、﹣1、0、1,
所以答案是:﹣3、﹣2、﹣1、0、1;
【考点精析】根据题目的已知条件,利用解一元一次方程的步骤和数轴的相关知识可以得到问题的答案,需要掌握先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;数轴是规定了原点、正方向、单位长度的一条直线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以正方形ABCD的一边向形外作等边△ABE,BD与EC交于点F,则∠AFD等于( )
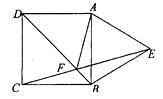
A.60°
B.50°
C.45°
D.40° -
科目: 来源: 题型:
查看答案和解析>>【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是90分,请问小红在竞赛中答对了多少道题?
(2)小明也参加了竞赛,考完后他说:“这次竞赛我一定能拿到100分.”请问小明有没有可能拿到100分?试用方程的知识来说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中生的参与情况,绘制了如下两幅不完整的统计图.请根据图中所给的信息解答下列问题:
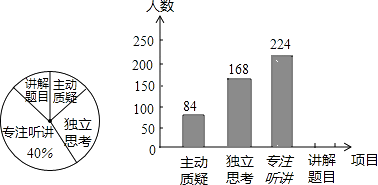
(1)这次评价中,一共抽查了名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=45°,AB=8,要使满足条件的△ABC惟一确定,那么BC的长度x的取值范围是 .
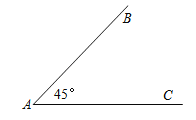
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一副三角板的直角顶点O重叠在一起.
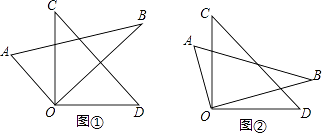
(1)问题发现:如图①,当OB平分∠COD时,∠AOD+∠BOC的度数是;
(2)拓展探究:如图②,当OB不平分∠COD时,∠AOD+∠BOC的度数是多少?
(3)问题解决:当∠BOC的余角的4倍等于∠AOD时,求∠BOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( )

A.52cm
B.40cm
C.39cm
D.26cm
相关试题

