搜索
【题目】如图，四边形ABCD的四边相等，且面积为120cm2 ， 对角线AC=24cm，则四边形ABCD的周长为（ ） 
A.52cm
B.40cm
C.39cm
D.26cm
参考答案：
【答案】A
【解析】解： 如图，连接AC、BD相交于点O，
∵四边形ABCD的四边相等，
∴四边形ABCD为菱形，
∴AC⊥BD，S四边形ABCD= 
ACBD，
∴ ×24BD=120，解得BD=10cm，
∴OA=12cm，OB=5cm，
在Rt△AOB中，由勾股定理可得AB= 
=13（cm），
∴四边形ABCD的周长=4×13=52（cm），
故选A．
可定四边形ABCD为菱形，连接AC、BD相交于点O，则可求得BD的长，在Rt△AOB中，利用勾股定理可求得AB的长，从而可求得四边形ABCD的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】据图回答下列问题
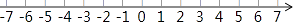
（1）数轴上表示5与﹣2两点之间的距离是 ，
（2）数轴上表示x与2的两点之间的距离可以表示为 ．
（3）如果|x﹣2|=5，则x= ．
（4）同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和，请你找出所有符合条件的整数x，使得|x+3|+|x﹣1|=4，这样的整数是 ．
（5）由以上探索猜想对于任何有理数x，|x﹣3|+|x﹣6|是否有最小值？如果有，直接写出最小值；如果没有，说明理由． -
科目： 来源： 题型：
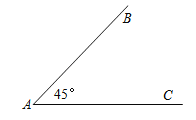
查看答案和解析>>【题目】如图，∠BAC=45°，AB=8，要使满足条件的△ABC惟一确定，那么BC的长度x的取值范围是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把一副三角板的直角顶点O重叠在一起．
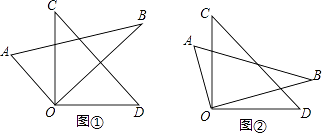
（1）问题发现：如图①，当OB平分∠COD时，∠AOD+∠BOC的度数是；
（2）拓展探究：如图②，当OB不平分∠COD时，∠AOD+∠BOC的度数是多少？
（3）问题解决：当∠BOC的余角的4倍等于∠AOD时，求∠BOC的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=3(x -5)2的图象上有两点P(2，y1)，Q(6，y2)，则y1和y2的大小关系是__________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直线L上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4 ， 则S1+2S2+2S3+S4=（ ）
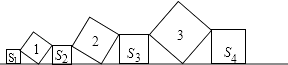
A.5
B.4
C.6
D.10 -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两人在太阳光下行走，同一时刻他们的身高与其影长之比的关系是___________
相关试题
