【题目】如图,在平面直角坐标系中,已知线段 AB 的两个端点坐标分别为A(a,5),B(8,b),且![]() .
.

(1)求 a,b 的值;
(2)①连OA,OB,则SAOB = 平方单位;(说明:SAOB 表示三角形 AOB 的面积,下同.)
②点P从O点出发沿 y 轴负方向运动,速度为每秒1个单位,连PA交OB于C,则运动多少秒时,SABC=SPOC ;
(3)在(2)的条件下,过P作直线m∥AB,过B作直线 l∥x轴,直线m和直线l相交于点Q,请直接写出点Q的坐标 .
参考答案:
【答案】(1)a=4,b=2;(2)①12,②8;(3)![]()
【解析】
(1)根据二次根式的性质即可求解.
(2)①利用割补法即可求出三角形 AOB 的面积;②利用待定系数法得出直线OA的解析式为![]() ,因为
,因为![]() ,所以BP∥OA,设点P从O点出发沿y轴负方向运动t秒时,OP=t,即P(0,-t),得出直线BP的解析式为
,所以BP∥OA,设点P从O点出发沿y轴负方向运动t秒时,OP=t,即P(0,-t),得出直线BP的解析式为![]() ,把B(8,2)代入即可.
,把B(8,2)代入即可.
(3)设直线AB的解析式为![]() ,把A(4,5)、B(8,2)代入,得到直线AB的解析式为
,把A(4,5)、B(8,2)代入,得到直线AB的解析式为![]() ,在(2)的条件下,P(0,-8),过P作直线m∥AB,过B作直线l∥x轴,直线m和直线l相交于点Q,则直线PQ的解析式为
,在(2)的条件下,P(0,-8),过P作直线m∥AB,过B作直线l∥x轴,直线m和直线l相交于点Q,则直线PQ的解析式为![]() ,点Q的纵坐标为2, y=2代入即可求解.
,点Q的纵坐标为2, y=2代入即可求解.
解:(1)∵![]()
而![]()
∴![]()
∴a-2b=0,b-2=0
解得:a=4,b=2
(2)①由(1)知:A(4,5)、B(8,2)
∴![]()
②设直线OA的解析式为![]() ,把A(4,5)代入,得
,把A(4,5)代入,得
![]()
![]()
∴直线OA的解析式为![]()
∵![]()
∴![]() +
+![]() =
=![]() +
+![]() ,即
,即![]() =
=![]()
∴BP∥OA
设点P从O点出发沿y轴负方向运动t秒时,
OP=t,即P(0,-t)
∴直线BP的解析式为![]() ,把B(8,2)代入,得
,把B(8,2)代入,得
![]()
t=8
∴点P从O点出发沿y轴负方向运动8秒时,![]()
(3)设直线AB的解析式为![]() ,把A(4,5)、B(8,2)代入,得
,把A(4,5)、B(8,2)代入,得

解得: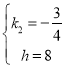
∴直线AB的解析式为![]()
在(2)的条件下,P(0,-8),过P作直线m∥AB,过B作直线l∥x轴,直线m和直线l相交于点Q,则直线PQ的解析式为![]() ,
,
点Q的纵坐标为2,当y=2时,![]()
解得:![]()
∴点Q的坐标为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识链接:将两个含30°角的全等三角尺放在一起,让两个30°角合在一起成60°,经过拼凑、观察、思考,探究出“直角三角形中30°角所对的直角边等于斜边的一半”结论.
如图:等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P,设运动时间为x秒.
(1)请直接写出AD长.(用x的代数式表示)
(2)当△ADE为直角三角形时,运动时间为几秒?
(2)求证:在运动过程中,点P始终为线段DE的中点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若有理数 a,b 满足
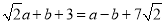 ,则a=____, b=____.
,则a=____, b=____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,△ABC满足∠BCA=90°,AC=BC=
 ,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.(1)当AB∥y轴时,求B点坐标.
(2)随着A、C的运动,当点B落在直线y=3x上时,求此时A点的坐标.
(3)在(2)的条件下,在y轴上是否存在点D,使以O、A、B、D为顶点的四边形面积是4?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在四边形ABCD中,AD=BC且AC⊥BD,点E,F,G,H,P,Q分别是AB,BC,CD,DA,AC,BD的中点.
求证:(1)四边形EFGH是矩形;
(2)四边形EQGP是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知 CD⊥AB,EF⊥AB,垂足分别为D,F,∠B+∠BDG=180°, 试说明∠BEF=∠CDG.将下面的解答过程补充完整,并填空(填写理由依据或数学式, 将答案按序号填在答题卷的对应位置内)
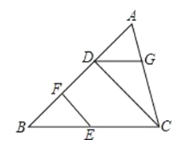
证明:∵CD⊥AB,EF⊥AB( ① )
∴∠BFE=∠BDC=90°( ② )
∴EF∥CD( ③ )
∴∠BEF= ④ ( ⑤ )
又∵∠B+∠BDG=180°( ⑥ )
∴BC∥DG( ⑦ )
∴∠CDG= ⑧ ( ⑨ )
∴∠CDG=∠BEF( ⑩ )
相关试题

