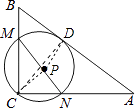
【题目】如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为 . 
参考答案:
【答案】![]()
【解析】解:如图,设MN的中点为P,⊙P与AB的切点为D,连接PD,连接CP,CD,则有PD⊥AB;
∵AB=13,AC=12,
∴BC= ![]() =5.
=5.
∵PC+PD=MN,
∴PC+PD≥CD,MN≥CD.
∴当MN=CD时,MN有最小值.
∵PD⊥AB,
∴CD⊥AB.
∵ ![]() ABCD=
ABCD= ![]() BCAC,
BCAC,
∴CD= ![]() =
= ![]() =
= ![]() .
.
∴CD的最小值 ![]() .
.
∴MN的最小值为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50个计算器时,买哪种品牌的计算器更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识链接:将两个含30°角的全等三角尺放在一起,让两个30°角合在一起成60°,经过拼凑、观察、思考,探究出“直角三角形中30°角所对的直角边等于斜边的一半”结论.
如图:等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P,设运动时间为x秒.
(1)请直接写出AD长.(用x的代数式表示)
(2)当△ADE为直角三角形时,运动时间为几秒?
(2)求证:在运动过程中,点P始终为线段DE的中点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若有理数 a,b 满足
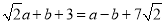 ,则a=____, b=____.
,则a=____, b=____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知线段 AB 的两个端点坐标分别为A(a,5),B(8,b),且
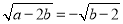 .
.
(1)求 a,b 的值;
(2)①连OA,OB,则SAOB = 平方单位;(说明:SAOB 表示三角形 AOB 的面积,下同.)
②点P从O点出发沿 y 轴负方向运动,速度为每秒1个单位,连PA交OB于C,则运动多少秒时,SABC=SPOC ;
(3)在(2)的条件下,过P作直线m∥AB,过B作直线 l∥x轴,直线m和直线l相交于点Q,请直接写出点Q的坐标 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,△ABC满足∠BCA=90°,AC=BC=
 ,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.(1)当AB∥y轴时,求B点坐标.
(2)随着A、C的运动,当点B落在直线y=3x上时,求此时A点的坐标.
(3)在(2)的条件下,在y轴上是否存在点D,使以O、A、B、D为顶点的四边形面积是4?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在四边形ABCD中,AD=BC且AC⊥BD,点E,F,G,H,P,Q分别是AB,BC,CD,DA,AC,BD的中点.
求证:(1)四边形EFGH是矩形;
(2)四边形EQGP是菱形.

相关试题

