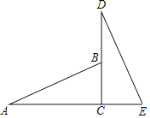
【题目】如图,已知C是线段AE上一点,![]() ,
,![]() ,B是CD上一点,CB=CE
,B是CD上一点,CB=CE
![]() 1
1![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 2
2![]() 若∠E=65°,求∠A的度数;
若∠E=65°,求∠A的度数;
![]() 3
3![]() 若AE=11,BC=3,求BD的长,
若AE=11,BC=3,求BD的长,![]() 直接写出结果
直接写出结果![]()
参考答案:
【答案】(1)见解析;(2)∠A=25°;(3)BD=5.
【解析】
(1)由“SAS”可证△ACB≌△DCE;
(2)由全等三角形的性质和直角三角形的性质可得∠A的度数;
(3)根据题意可得AC=DC,BC=CE=3,根据线段和差即可求BD的长.
解(1)∵DC=AC,∠ACB=∠DCE=90°,BC=CE,
∴△ACB≌△DCE(SAS);
(2)∵△ACB≌△DCE,
∴∠E=∠ABC=65°,
∴∠A=90°∠ABC=25°;
(3)∵AC=DC,BC=CE=3,
∴CD=AC=AECE=113=8,
∴BD=CDBC=83=5.
-
科目: 来源: 题型:
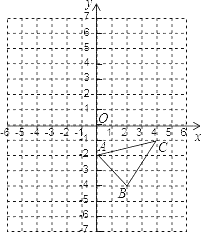
查看答案和解析>>【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB,AC的垂直平分线分别交BC于D,E两点,垂足分别是M,N.
(1)若△ADE的周长是10,求BC的长;
(2)若∠BAC=100°,求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(
 )
) ,正六边形的边长为(
,正六边形的边长为( )cm(其中
)cm(其中 ),求这两段铁丝的总长
),求这两段铁丝的总长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
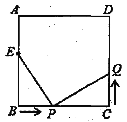
(1)若点Q的运动速度与点P的运动速度相等,经过 秒后,△BPE≌△CQP;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道
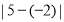 表示
表示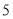 与
与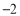 之差的绝对值,实际上也可理解为
之差的绝对值,实际上也可理解为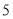 与
与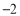 两数在数轴上所对的两点之间的距离,试探索:
两数在数轴上所对的两点之间的距离,试探索:(1)求
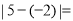 __________.
__________.(2)找出所有符合条件的整数
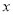 ,使得
,使得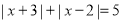 .满足条件的所有整数值有___________
.满足条件的所有整数值有___________(3)由以上探索,猜想对于任何有理数
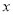 ,
,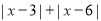 是否有最大值或最小值?如果有最大值或最小值是多少?
是否有最大值或最小值?如果有最大值或最小值是多少?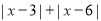 有最__________(填“最大”或“最小”)值是__________.
有最__________(填“最大”或“最小”)值是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为
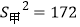 ,
, 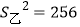 .下列说法:
.下列说法: ①两组的平均数相同;
②甲组学生成绩比乙组学生成绩稳定;
③甲组成绩的众数>乙组成绩的众数;
④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好.其中正确的共有( )
分数
50
60
70
80
90
100
人
数甲组
2
5
10
13
14
6
乙组
4
4
16
2
12
12
A. 2种 B. 3种 C. 4种 D. 5种
相关试题

