【题目】求证:相似三角形对应边上的中线之比等于相似比.
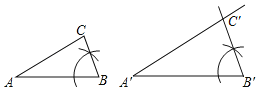
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

参考答案:
【答案】(1)作图见解析;(2)证明见解析.
【解析】
(1)作∠A'B'C=∠ABC,即可得到△A'B′C′;
(2)依据D是AB的中点,D'是A'B'的中点,即可得到![]() ,根据△ABC∽△A'B'C',即可得到
,根据△ABC∽△A'B'C',即可得到![]() ,∠A'=∠A,进而得出△A'C'D'∽△ACD,可得
,∠A'=∠A,进而得出△A'C'D'∽△ACD,可得![]() .
.
(1)如图所示,△A'B′C′即为所求;
(2)已知,如图,△ABC∽△A'B'C',![]() =k,D是AB的中点,D'是A'B'的中点,
=k,D是AB的中点,D'是A'B'的中点,
求证:![]() =k.
=k.
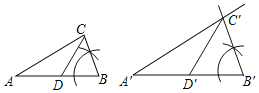
证明:∵D是AB的中点,D'是A'B'的中点,
∴AD=![]() AB,A'D'=
AB,A'D'=![]() A'B',
A'B',
∴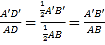 ,
,
∵△ABC∽△A'B'C',
∴![]() ,∠A'=∠A,
,∠A'=∠A,
∵![]() ,∠A'=∠A,
,∠A'=∠A,
∴△A'C'D'∽△ACD,
∴![]() =k.
=k.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在日常生活中,如取款、上网等都需要密码,有一种利用“因式分解”产生的密码,方便记忆,原理是:如多项式
 ,若
,若 ,
, 时,则各因式的值为
时,则各因式的值为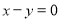 ,
, ,
, ,于是把018162作为一个六位数的密码,对于多项式
,于是把018162作为一个六位数的密码,对于多项式 ,取
,取 ,
, 时,用上述方法产生的密码是_________________.(写一个即可)
时,用上述方法产生的密码是_________________.(写一个即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+m与双曲线y=
 相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC面积的最小值为_____.
相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC面积的最小值为_____.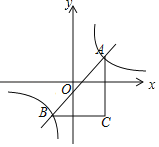
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把等边三角形
 沿着
沿着 折叠,使点
折叠,使点 恰好落在
恰好落在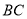 边上的点
边上的点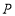 处,且
处,且 。若
。若 ,
, ,则
,则 ______
______ .(在直角三角形中,
.(在直角三角形中, 角所对的直角边等于斜边的一半。)
角所对的直角边等于斜边的一半。)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等边
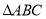 中,点
中,点 、
、 分别在
分别在 、
、 上,
上, ,连
,连 、
、 .
.
(1)求证:
 ;
;(2)如图2,延长
 至点
至点 ,使得
,使得 ,连
,连 ,试判断
,试判断 的形状,并说明理由;
的形状,并说明理由;(3)在(2)的条件下,连
 ,
, .若
.若 ,则
,则 ______.
______.
相关试题

