【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ![]() ,求大楼AB的高度是多少?(精确到0.1米,参考数据:
,求大楼AB的高度是多少?(精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.45)
≈2.45)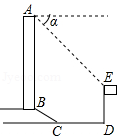
参考答案:
【答案】解:延长AB交DC于H,作EG⊥AB于G,如图所示: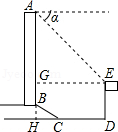
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1: ![]() ,
,
∴BH:CH=1: ![]() ,
,
设BH=x米,则CH= ![]() x米,
x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+( ![]() x)2=122 ,
x)2=122 ,
解得:x=6,
∴BH=6米,CH=6 ![]() 米,
米,
∴BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=6 ![]() +20(米),
+20(米),
∵∠α=45°,
∴∠EAG=90°﹣45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6 ![]() +20(米),
+20(米),
∴AB=AG+BG=6 ![]() +20+9≈39.4(米).
+20+9≈39.4(米).
故大楼AB的高度大约是39.4米.
【解析】延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CH= ![]() x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6
x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6 ![]() 米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6
米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6 ![]() +20(米),即可得出大楼AB的高度.
+20(米),即可得出大楼AB的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在网格中有一个四边形图案.
(1)请你画出此图案绕点O按顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1,A2,A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交
 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D. 
(1)求证:DC=DP;
(2)若直径AB=12cm,∠CAB=30°, ①当E是半径OA中点时,切线长DC=cm:
②当AE=cm时,以A,O,C,F为顶点的四边形是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2011贵州安顺,10,3分)一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )

A. (4,O) B. (5,0) C. (0,5) D. (5,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为( )

A. 115° B. 120° C. 125° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图数在线的A、B、C三点所表示的数分别为a、b、c.根据图中各点位置,判断下列各式何者正确( )

A. (a﹣1)(b﹣1)>0 B. (b﹣1)(c﹣1)>0 C. (a+1)(b+1)<0 D. (b+1)(c+1)<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )

A. 110° B. 120° C. 130° D. 140°
相关试题

