【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
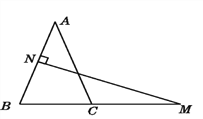
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
参考答案:
【答案】(1) 20°;(2) 35°;
(3)规律:∠NMB=![]() ∠A.
∠A.
【解析】(1)根据等边对等角,由AB=AC可得到∠ABM=∠ACB,再结合已知∠A的度数,即可求出∠NMB的度数;
(2)仿照第(1)问的求解过程即可得到∠NMB的度数;
(3)结合上述两问的解答,即可发现∠NMB和∠A之间的大小关系,然后仿照上述解答过程进行验证即可.
解:(1)∵AB=AC,
∴∠ABM=∠ACB.
∵∠BAC=40°,∠ABM=∠ACB,
∴∠ABM=![]() ×(180°-∠BAC)=70°.
×(180°-∠BAC)=70°.
∵MN是AB的垂直平分线,∠ABM=70°,
∴∠NMB=90°-∠ABM=90°-70°=20°.
(2)与(1)同理可得∠B=![]() ×(180°-∠BAC)=55°,
×(180°-∠BAC)=55°,
∴∠NMB=90°-55°=35°.
(3)规律:在等腰△ABC中,当AB=AC,∠NMB的度数恰好为顶角∠A度数的一半,即∠NMB=![]() ∠A.理由如下:
∠A.理由如下:
∵AB=AC,
∴∠ABM=∠ACB.
∴∠ABM=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∵∠ABM=90°-![]() ∠A,∠BNM=90°,
∠A,∠BNM=90°,
∴∠BMN=90°-∠ABM=![]() ∠A.
∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x+1)(x﹣m)交x轴于A,B两点(A在B的左侧,m>0),交y轴正半轴于点C,过点C作x轴的平行线交抛物线于另一点E,抛物线的对称轴交CE于点F,以C为圆心画圆,使⊙C经过点(0,2).
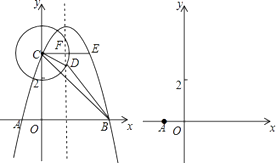
(1)直接写出OB,OC的长.(均用含m的代数式表示)
(2)当m>2时,判断点E与⊙C的位置关系,并说明理由.
(3)当抛物线的对称轴与⊙C相交时,其中下方的交点为D.连结CD,BD,BC.
①当m>3,且C,D,B三点在同一直线上时,求m的值.
②当△BCD是以CD为腰的等腰三角形时,求m的值.(直接写出答案即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点C顺时针旋转90°得到△A2B2C2.
(2)回答下列问题:
①△A1B1C1中顶点A1坐标为 ;
②若P(a,b)为△ABC边上一点,则按照(1)中①作图,点P对应的点P1的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】两瓶酒精,甲瓶有
 升,浓度未知;乙瓶有
升,浓度未知;乙瓶有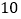 升,浓度
升,浓度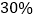 ,从甲瓶中倒入乙瓶
,从甲瓶中倒入乙瓶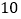 升酒精,摇匀后倒回一部分给甲瓶,此时甲瓶浓度为
升酒精,摇匀后倒回一部分给甲瓶,此时甲瓶浓度为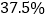 ,乙瓶浓度为
,乙瓶浓度为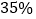 ,此时乙瓶中有酒精( )升.
,此时乙瓶中有酒精( )升.A. 5 B. 6.3 C. 5.25 D. 5.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】用
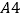 纸在某誊印社复印文件,复印页数不超过
纸在某誊印社复印文件,复印页数不超过 时每页收费
时每页收费 元;复印页数超过
元;复印页数超过 时,超过部分每页收费
时,超过部分每页收费 元.在某图书馆复印同样的文件,不论复印多少页,每页收费
元.在某图书馆复印同样的文件,不论复印多少页,每页收费 元,如何根据复印的页数选择复印的地点使总价格比较便宜?
元,如何根据复印的页数选择复印的地点使总价格比较便宜? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
相关试题

