【题目】如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P; 
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由. 
参考答案:
【答案】
(1)解:∵BC⊥AE,∠BAE=45°,
∴∠CBA=∠CAB,
∴BC=CA,
在△BCE和△ACD中,
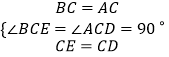
∴△BCE≌△ACD,
∴AD=BE.
(2)解:∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BDP=∠ADC,
∴∠BPD=∠DCA=90°,
∵AB=AE,
∴AD平分∠BAE.
(3)解:AD⊥BE不发生变化.
如图2,
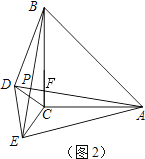
∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BFP=∠ACF,
∴∠BPF=∠ACF=90°,
∴AD⊥BE.
【解析】(1)利用SAS证明△BCE≌△ACD,根据全等三角形的对应边相等得到AD=BE.(2)根据△BCE≌△ACD,得到∠EBC=∠DAC,由∠BDP=∠ADC,得到∠BPD=∠DCA=90°,利用等腰三角形的三线合一,即可得到AD平分∠BAE;(3)AD⊥BE不发生变化.由△BCE≌△ACD,得到∠EBC=∠DAC,由对顶角相等得到∠BFP=∠ACF,根据三角形内角和为180°,所以∠BPF=∠ACF=90°,即AD⊥BE.
-
科目: 来源: 题型:
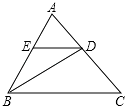
查看答案和解析>>【题目】如图所示,△ABC中,BD是∠ABC的平分线,DE∥BC,交AB于点E,∠A=60°,∠BDC=95°,求△BDE各内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
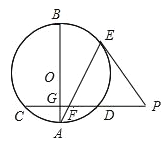
(1)求证:PE=PF
(2)已知AG=4,AF=5,EF=25,求圆O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是∠AOB平分线上的点,EC⊥OA于点C,ED⊥OB于点D,连接CD,求证:
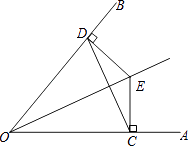
(1)∠ECD=∠EDC;
(2)OE是线段CD的垂直平分线. -
科目: 来源: 题型:
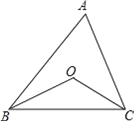
查看答案和解析>>【题目】如图,已知点O是△ABC的两条角平分线的交点,
(1)若∠A=30°,则∠BOC的大小是 ;
(2)若∠A=60°,则∠BOC的大小是 ;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )
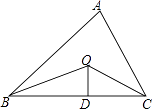
A.25
B.84
C.42
D.21 -
科目: 来源: 题型:
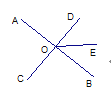
查看答案和解析>>【题目】如图3,直线AB、CD相交于O,若∠AOD比∠AOC大40°,则∠BOD=___°;若∠AOD=2∠AOC,则∠BOC=___;若∠AOD=∠AOC,则∠BOD=___.
相关试题

