搜索
【题目】如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于，且OD=4，△ABC的面积是（ ）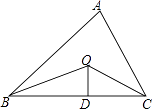 
A.25
B.84
C.42
D.21
参考答案：
【答案】C
【解析】解：连接OA，作OE⊥AB于E，OF⊥AC于F，如图， ∵OB，OC分别平分∠ABC和∠ACB，
∴OD=OE=4，OD=OF=4，
∴△ABC的面积=
S△AOB+S△BOC+S△AOC
= 
OEAB+ ODBC+ OFAC
= ×4×（AB+BC+AC）
= ×4×21
=42．
故选C．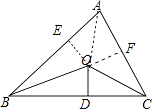
【考点精析】通过灵活运用角平分线的性质定理，掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点E是∠AOB平分线上的点，EC⊥OA于点C，ED⊥OB于点D，连接CD，求证：
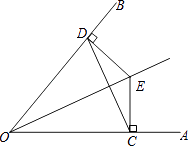
（1）∠ECD=∠EDC；
（2）OE是线段CD的垂直平分线． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ABE是等腰三角形，AB=AE，∠BAE=45°，过点B作BC⊥AE于点C，在BC上截取CD=CE，连接AD、DE并延长AD交BE于点P；
（1）求证：AD=BE；
（2）试说明AD平分∠BAE；
（3）如图2，将△CDE绕着点C旋转一定的角度，那么AD与BE的位置关系是否发生变化，说明理由．
-
科目： 来源： 题型：
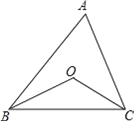
查看答案和解析>>【题目】如图，已知点O是△ABC的两条角平分线的交点，
（1）若∠A=30°，则∠BOC的大小是 ；
（2）若∠A=60°，则∠BOC的大小是 ；
（3）若∠A=n°，则∠BOC的大小是多少？试用学过的知识说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图3，直线AB、CD相交于O，若∠AOD比∠AOC大40°，则∠BOD=___°；若∠AOD=2∠AOC，则∠BOC=___；若∠AOD=∠AOC，则∠BOD=___.
-
科目： 来源： 题型：
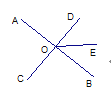
查看答案和解析>>【题目】已知如图，直线AB、CD相交于O，OE平分∠BOD，OF平分∠COB，∠2∶∠1=4∶1，求∠AOF的度数.
解：∵OE平分∠BOD
∴∠BOD=＿＿∠1
∵
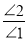=4 ∴∠2=＿＿∠1
∵∠2＋∠BOD=＿＿＿＿
∴4∠1+2∠1=
∴∠1=30°
∴∠BOD = ；
∴∠AOC= ；
又∵∠BOD+∠BOC=180°
∴∠BOC=120°
∵ OF平分∠COB
∴∠COF=∠BOF= ；
∴∠AOF=60°+60°= .
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC沿直线L对折后能与△ADC重合，且AB∥CD，下列选项正确的是（ ）
A.AB=CD，AO=OC
B.AB=BD，∠BAD=∠DCB
C.AB∥BC，BC=BD
D.OD=OB，∠CDB=∠BCD
相关试题
