【题目】如图,点E是∠AOB平分线上的点,EC⊥OA于点C,ED⊥OB于点D,连接CD,求证: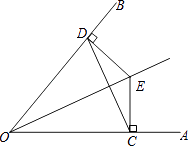
(1)∠ECD=∠EDC;
(2)OE是线段CD的垂直平分线.
参考答案:
【答案】
(1)
解:∵OE是∠AOB的平分线,EC⊥OA,ED⊥OB,
∴EC=ED,
∴∠ECD=∠EDC;
(2)
解:在Rt△ODE和Rt△OCE中,
∵ ![]() ,
,
∴Rt△ODE≌Rt△OCE(HL),
∴OC=OD,
又∵DE=CE,
∴OE是CD的垂直平分线.
【解析】(1)由角平分线的性质即可得证;(2)根据“HL”证Rt△ODE≌Rt△OCE,得OC=OD,由DE=CE可得OE是CD的垂直平分线.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对线段垂直平分线的性质的理解,了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .

-
科目: 来源: 题型:
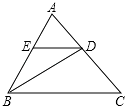
查看答案和解析>>【题目】如图所示,△ABC中,BD是∠ABC的平分线,DE∥BC,交AB于点E,∠A=60°,∠BDC=95°,求△BDE各内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
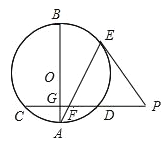
(1)求证:PE=PF
(2)已知AG=4,AF=5,EF=25,求圆O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;

(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
-
科目: 来源: 题型:
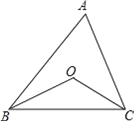
查看答案和解析>>【题目】如图,已知点O是△ABC的两条角平分线的交点,
(1)若∠A=30°,则∠BOC的大小是 ;
(2)若∠A=60°,则∠BOC的大小是 ;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
-
科目: 来源: 题型:
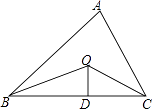
查看答案和解析>>【题目】如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )
A.25
B.84
C.42
D.21
相关试题

